Partial Fraction Example 6
Raw Transcript
Hello Everyone, Tom from everystepcalculus.com and everystepphysics.com. I’m going to do a test problem on Partial Fraction Decomposition, again.Let me show you how my programs work on this. Index 8 to get to my main menu. And we scroll down the Partial Fractions which is in the menu. You can scroll up or down here with the cursor. You have to press Alpha before we enter anything in these entry lines here.Press Alpha and the problem is one divided by, I’m going to use parentheses for the denominator And numerator. This one is x squared minus nine.I always show you what you’ve entered. Now notice that x squared minus nine is a difference of squares so when you factor that it’s always X minus three times x plus three. And that’s a big deal in calculus so always always be on the lookout for these type of things. These difference of squares. Sometimes I’ll have X minus 3 up in the numerator and it will cancel and they use all kinds tricks to throw you off. If you’re hip and I’m gonna try to make you hip, you’re always are looking for the difference in squares. Okay. We’re doing Partial Fractions so I say it’s okay. I’ll always give you a change it if it’s not. And I factor it for you. Here’s x minus three times x plus three. If you can’t factor the denominator, you can’t do Partial Fractions. So keep that in mind, too. And the problems have to be relatively simple in tests because not that many people, including myself, are not very good factoring. In our heads, you know. They get more complicated than this, so. So, you start out by putting one,numerator, divided by x squared minus 9 times x squared minus nine. What you’re doing is multiplying both sides the denominator. This is factored but this is not. And of course, when you multiply the numerator by this, you’re going to eliminate. So there’s going to b one up there. And of course these switch around as we do times this portion here. A divided by x minus three plus B divided by x plus three. I switched it around now so it’s one equals A times x plus three plus b times x minus three. Now the first thing you want to do is eliminate some of these. So you’re going to put a minus three here to make this zero. I’ll do that for you. I have x equals minus three. I put, anytime you see quotation marks, you put parentheses. Parentheses minus three plus three which is zero. B times parentheses minus three parentheses minus three which is minus 6. Zero minus six so one equals a B minus 6. One equals B minus 6 to B is equal to minus one sixth. And X equals three parentheses three in here. open and close plus three And this becomes six and this becomes zero. Which a is equal to one sixth. Partial Fractions, enter one sixth divided by by X minus three plus minus one sixth divided by X plus three. Those are the Partial Fractions. And when you integrate these, one sixth logged absolute value X minus three plus minus one sixth times log absolute value X plus 3. So add all the stuff on your paper and homework, or whatever. Get the problem perfect. Pretty neat, huh? everystepcalculus.com. Go to my site and buy my programs.
Thank you
Partial Fraction Decomposition Ex 11
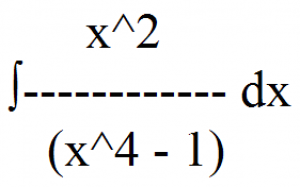
Partial Fractions Example 3
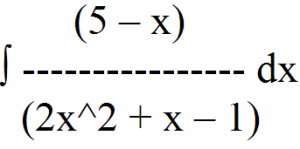
Partial Fractions of Integral-Video
Raw Transcript
Hello Everyone, Tom for everystepcalculus.com and everystepphysics.com. I’m going to do partial fraction problem. This person said that it’s a hard partial fraction problem. Let’s see about that. It is hard if you ask me, without my programs. But let’s do it. Index 8 to get to my menu. Scroll down to partial fractions. We’re going to enter the integral. You have to press alpha before you enter anything in these entry lines. We’re going to go alpha and then going to do left parentheses, X squared plus 3 times X plus 1 close off the parentheses divided by, open up the parentheses, X to the fourth power plus 5 times X squared plus 4, close off the parentheses.
I always show you what you’ve entered. Now maybe you’re better than I am but you have to factor this denominator in partial fractions every time. So this it makes it hard for a class in it for a test problem is way too hard for a test probably for homework because I don’t know who would be able to write off from memory to factor that. I say it’s okay. We factor the denominator; here it is right here. And we start doing our partials. The idea is that you are going to deliminate the denominator here by multiplying at times the same thing with the numerator this. This here is the the factored part ion is here and this is the original denominator. And so then we have
the numerator is equal to Ax plus B times x square plus 4 plus Cx plus D times x squared plus 1.You multiply that out using the foil method. Remember the foil method? First outside inside and last. First would be Ax times x squared,outside would be Ax times four, et cetera. I multiply it out here. The calculator uses small letters rather than capitals. No problem. They combine those terms and come up with this. A plus C is x squared, x squared, 4a plus c, et cetera. Now we have to figure out the coefficients for this numerator. And since there’s no X cubed, we have to put one in there, which is 0 times x cubed. And then we have one coefficient here, three coefficient here, and one. So here we have one, three, and one. So then therefore AC is equal to 0, BD equal to one. 4a plus c is equal to three and 4b plus d is equal to one. And we work out, we use subtraction. We’re subtracting like terms. So AC is subtracted. 4a plus c and that equals three. A equals one. Do the same for each one of them. D equals one, C equals a minus one. Notice here we’re replacing A with what we found which is one. Which I do that for you here. When they’re in quotation marks, I replaced it in there. Partial fractions are this. Right here. And I also do the integrals for you. Log of x squared plus one divided by two, et cetera, et cetera. Pretty neat, huh?
everystepcalculus.com. Go to my site and buy my programs.
Thank you
Partial Fractions
Let’s talk about partial fractions and what I’ve found out after programming them. Partial fractions would never occur in real life. Remember the integral is the area under a smooth curve, nothing more from my knowledge, when you graph any original function; it has at least 2 asymptotes. Well that eliminates the smooth curve. Remember an asymptote is a vertical line or sometimes horizontal line where the original function never touches to infinity, so if you choose a range that goes (crosses) over that asymptote there is no computed answer, so no area under a smooth curve. So partial fractions are a Sudoku of math problem, like so many of calculus problems. So let’s get into what I’ve found in programming this area of calculus. The denominator has to be factored to produce partial fractions. Sometimes there are two factors, then three, then two factors with an exponent in between the parenthesis, then even one factor with an exponent outside the parenthesis. The factored denominator is the key as to how to approach the problem.
In my programs, I have a whole separate program to decide if there are two factors or three or any other choices. Most of us are not good at factoring. Maybe simple functions we can, like the difference of squares (x^2-9) = (x-3)(x+3). When it gets a little deeper that this most of us are lost. For instance, what’s the factors of (x^3-x) or (x^4+7x^3+6x^2)? The calculator knows and because of that, so does my programs. But would those appear in your test? In my opinion if they did then most of the class would fail that. No question about it. Let alone complete the partial fractions. So enough about factoring. Remember in algebra when they said you could do anything to one side of an equation as long as you do it to the other side also. They do this in partial fractions. On the left side of the equation in partial fractions they multiply the original function by the denominator, which effectively gets rid of the denominator. Well they do the same thing on the other side (except factored) to get rid of the added or subtracted fractions, and change the A / (x-1) to a product through common denominator. That said, a few trick to remember in partial fractions. If in the factored denominator you have (x^2+6) for the first factor so you want to set that up for partial fractions you would go Ax+B / (x^2+6), if the second factor was (x^2-3) you’d set this up as (Cx+D) / (x^2-3), Do you understand this? Very important and no exceptions!! If the factor turned out to be (x-5)^5(exponent outside of the parenthesis), this is called re-occurring powers, or exponents, and the factors are A/(x-5)^1 + B/(x-5)^2+C/(x-5)^3+E/(x-5)^4+F/(x-5)^5. Now if the power in the denominator is less or equal to the power in the numerator, you have to use short division to find the remainder to the partials.
My programs do all of this for you, as I required my programming to do for me also when I was in class. Hey good luck in your class, I’m always available to help you if you just ask.
Partial Fractions Example 10-Video
Partial Fractions | Example 9-Video
Raw Transcript
Hello Everyone, Tom from everystepcalculus.com and everystepphysics.com. Partial Fraction Decomposition. This time with three Partial Fractions.Let’s get started.Put index 8 in here with the open and closed parentheses, you get to my menu.You can scroll down to start up in the a section but you can scroll down alphabetical to Partial Fractions.Enter the integral by pressing Alpha first. Alpha, parentheses X squared plus 12 times X plus 12,close off the parentheses, divided by, open parentheses X cubed minus 4 times X. I always show you what you’ve entered. How many of you could factor this here? It’s pretty tough, I would think. Do it easy on my program. It comes up with 3 factors. So you write this in your paper. X squared plus 12x plus 12 is the numerator. Divided by the denominator times the denominator. And this is the actual denominator factored so we do the same thing here. And we’re going to use this to multiply times all of this to get rid of all the divisions. Common denominator is the actual words. So we added with x squared plus 12x plus 12 equals A and x times x minus 2 times x plus 2 Bx times x plus 2 Cx times x minus 2 And x equals 2. These quotation marks here is what the calculator does but you would put parentheses wherever you see these. parentheses 2 squared. You’re substituting 2 for every x in these functions. Use parentheses 2 here plus 12, etc. Do that throughout the whole system here. And that turns out to be B equals 5. At x equals zero. Use 0 for every x in all the computations here. And that turns out to be A equals minus 3 and x equals minus 2. Substitute for x in all the equation. C equals minus 1. Partial Fractions are minus 3 over x plus 5 over x minus two plus minus one over x plus two. And we integrate those. One thing about integrating a denominator with no, no exponent. You notice you can’t. This is an exponent of one, theoretically. But if you try to switch it to the numerator, five times X minus 2, it becomes a minus 1. Well in integration, you’re going to add one and then divide by the result. Well if you add one to a minus one, you get zero. In the numerator, anything to the zero is one. So that’s the reason you have to use logs. Whenever you see a no exponent to the denominator, it’s a log integration. So minus three logged minus the absolute X 5 log absolute x minus two minus one log x plus 2 plus C. Pretty neat, huh? everystepcalculus.com
Go to my site and buy my programs.
Thank you for watching.
Partial Fraction Decomposition on TI-89
Partial Fraction Decomposition on TI-89
Raw Transcript
This is a video from EveryStepCalculus.com demonstrating how my programs work on a TI-89 Titanium calculator and other calculators in the TI system for physics and calculus problems.
Okay, Partial Fraction Decomposition. Let’s get started, to get to my menu you have to press 2nd alpha to put the i_n_d_e_x in here you have to press alpha to put the 9 (). Press Enter and you’re into my menu. Scroll down to wherever you want all the way up and down.
But I’m at Partial Fractions right now which we want to do and we’re going to enter our function. You always have to Press alpha before you enter anything in a these entry lines in my programs. So Alpha we’re gonna do a quantity of 4 times X plus 9, divided by the quantity X minus 1, times the quantity of x plus 1, times the quantity of X plus 4.
I always show you what you’ve entered so you can change in case you made a mistake and we’re into the problem. You factored the denominator. It’s already factored here but in case it wasn’t, I would. And then you multiply, you multiply by the factor of the denominator. You get these. They’re all exactly right. Mark it down on your paper exactly like you see it. And if x = 1, the idea is that you cancel certain factors, certain variables. And here’s when you put -1 the function here is where they all set.
Mark that on your paper, turns out to be 5=A*(0)+B*(-6)+C*(0) 5=B*(-6) 5/-6. Mark all that on your paper. X equals one which will negate the second term. You mark these all these… put all these in replace or um x in your function there. A couple of them become zeros so that you can solve so a equals 13 tenths. And then you have enough variables, enough answers to solve the other c. Here’s the answer.
Pretty neat, huh? EveryStepCalculus.com. Go to my site, buy my programs and pass calculus.
More Partial Fraction test questions solved on your TI-89 calculator
Partial Fraction Test Question #1
Partial Fraction Decomposition Video
Partial Fraction Decomposition on the TI-89
Raw Transcript
Hello everyone, Tom from everystepcalculus.com, going to do a partial fraction decomposition right now, letís get started.
Index 7 if you bought both programs and loaded them into the calculator with the instructions and youíre going to scroll to partial fractions, thatís what we want to do with the problem and weíre going to add our function, you have to press alpha before you add anything in this entry lines here. Alpha four divided by parenthesis parenthesis three times X minus one close up parenthesis times X and it will show you what youíve entered and notice this is already factored, this is actually three X squared minus X but itís already been factored here in this problem and we say itís ok, it allows you to change it in case you made a mistake, so here is the factoring of it, you always the denominator, if the denominator canít be factored itís not a partial fraction *** your problem, then we go through the calculations. A is over X and B is over 3X-1 and we multiply times the factoring because we want to eliminate this from the other side, when we multiply something thatís been divided we can eliminate it and it also makes these into linear variables such as this and then we try to make one zero so we could solve for the other one which we do here and B equals 12, Iíll go through it quick, now we have X equal to zero and so A equals -4 and hereís the answer, the partial fraction here is -4/X + 12 and when you do the X integration of it, it becomes a log problem and I do that for you too, -4 log of log of absolute value of X + 12 log of 3X, pretty neat, everystepcalculus.com, go to my site, buy my programs, pass your calculus class and also subscribe to new videos if you want at my channel.
Partial Fractions 4 on the Ti89 | Every Step Calculus Video
Partial Fractions Decomposition 4 on TI-89
Raw Transcript
This is a video from EveryStepCalculus.com demonstrating how my programs work on a TI 89 Titanium calculator and other calculators in a TI system for physics and calculus problems.
Okay, partial fraction decomposition. All my programs work on, many people have asked for that so I programmed it. Um, to get to my menu you have two press second Alpha to put I_N_D_E_X. This is a calculus two and three Series and then you have to press Alpha again to put the 9 in the open and close parentheses and press Enter and then your into my menu.
I’m already at partial fractions here all are alphabetical you scroll down to it. Choose that, press Enter, give an example with what it should look like. When you enter it you have to press Alpha before you enter anything in these empty lines here.
Going to go Alpha for quantity, you have to use parenthesis now. We’re doing quantities in numerators and quantities in denominators. So the quantity X squared plus 8 divided by quantity X squared minus 5 times X plus six now you want to do this without from memory without my programs be my guest.
I always show you what you’ve entered, so you can change in case you made a mistake I say it’s okay and the first thing you do is factor the denominator which is this. You write this on your paper exactly as you see it and so the numerator is equal to these but put the a and b partial fractions in. You multiply it times the common denominator. Actually this is on the other side to x squared plus eight over this amount but when you multiply it out it cancels and x squared plus 8 equals a times X minus 2 plus b X minus 3.
You choose a number that will cancel the one of them, so you can solve it and you choose 2 so you got your, these in quotation marks are entered for the x’s x squared plus 8 here’s 2 minus 2 etcetera. You write that on your paper. I show you what the answer is and you work it out and you come up with b minus 12. And you write down on your paper, that x equals three.
Mark that into the equation and it equals this and then you work out the computations in a equals 17 so the partial fractions 17 over x-3 plus -12 or x-2.
Pretty neat huh, EveryStepCalculus.com go to my site by my programs and pass calculus.
Partial Fractions Decomposition Video
Raw Transcript
This is a video from EveryStepCalculus.com demonstrating how my programs work on a TI-89 Titanium calculator and other calculators in the TI system for physics and calculus problems
okay partial fractions. Uh, to get started on my programs you have to press 2nd Alpha to put in i_n_d_e_x in here then press. Alpha to put the 9 in open and close parentheses press enter and your into my menu. I’m already at partial fractions you see there’s a menu here, all alphabetical that
you can scroll down to up to we want partial fractions right now you have to press Alpha before you put in anything into these entry lines here remember to press Alpha and put in the function 1 divided by the quantity x squared plus 2 times x, I’ve already showed you what you’ve entered so you can change it if you want. I say it’s okay first of all we factor the denominator it’s already factored here and we choose our A&B and b would be x and x plus 2, equals 1 and then we multiply by the common denominator which I showed you in the previews one you get x, or a times x plus 2 plus b times x trying to eliminate one parameters one variable a in this case so we multiply by a -2 or I mean add by a -2 we’ll get a zero so we choose that one and then we figure out what b is, and then we can use that to figure out what a is and here’s a and your three halves, here’s your partial thing for your answer for your calculus test pretty neat huh? EveryStepCalculus.com goto my site buy my programs and pass calculus.