Every Step Calculus

Show Work Step by Step on your TI-89 Calculator Screen

Home » Calculus 3

Partial Derivatives First Order

by Leave a Comment

Raw Transcript

Hello again, everyone, this is Tom from everystepcalculus.com and everystepphysics.com. I’m gonna do partial derivatives now in this video, generally with respect to calculus 2 or 3. Let’s do it. Index 8, get to my menu… Scroll up to get to the P’s quicker. It goes to the bottom of the alphabet, so we get to what we’re looking for, it’s partial derivatives. On the menu you can go second and the titanium second and then these cursers to go page by page. You do that here to get through the menu quicker, and we’re looking at, let’s see, partial fractions, here’s partial derivatives, and I programmed first order or second order; we’re going to do first order in this problem. Z= f (x,y) We’re going to enter our function, that the function given is. You have to press alpha before you enter anything into these entry lines in my programs, okay, so alpha, and then we’re going to press T here, which gives us the arc tangent for Y divided by X I always show you what you’ve entered so you can change it if you made a mistake. So it’s okay, and here’s the partial derivatives, with respect to x, is minus Y divided by X squared plus Y squared, this is a, if you go to my trig identities you’ll see that tangent to the minus 1 is 1 over the quantity of 1 plus x squared. In this case it would be 1 over the quantity 1 plus Y divided by X squared. To get the derivative with respect to X and with respect to Y, it’s this equation here. And then there’s a point A and B that they give you. Press the one for A, is alpha, minus 2. Make sure you know it’s interchanged the minus sign for the negative sign. And then for the B, alpha 7 is given. Again I’ll show you what you’ve entered, and we see that’s okay, and so the problem asks for fx(a,b), which is this right here, replacing the y’s and the x’s for whatever is given here for A and B. And I have to use quotation marks the way the calculator allows me to with programming, but you’re going to use parentheses here anytime you see a quotation here, because you’re substituting X and Y values for the X and Y values in the function. And the answer is -7 over 53. And now if they ask you for F of Y you’d go one step further, and that would be substituting this, you get -2 over 53. Pretty neat, huh? everystepcalculus.com, go to my site and subscribe to me so you can see other videos if you’re interested. Have a good one!

Triple Integral: Work Shown on TI89-Video

by Leave a Comment

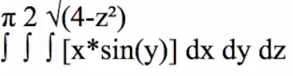
Screen shot 2015-02-04 at 12.32.17 PM

 

 

 

Transcripts

Hello again, everyone. This is Tom from everystepcalculus.com and everystepphysics.com. I’m going to do a Triple Integral for Calculus 3 right now. This is an example of a Patrick JMT, my favorite instructor on the internet, on YouTube. So I’m going to show you how it works on my program. I don’t know anybody can do that problem. He can do it because he’s a genius. But for us students,etc. How do we do it? Let’s get started. Index 8 to get to my menu. I’m going to scroll up because I can go to the bottom of the menu then instead of going down quicker to go to the T’s section. And we’re going to choose Triple Integral. And we’re going to enter our function. You have to press Alpha before you enter anything into these entry lines here in programs, okay. Alpha x times sin of Y. I always show you what you’ve entered. You can change it if you want. And we’re going to use the order of integration which is dx, dz, dy which is in the example. You have the other choices in case that’s given on test also. And we’re going to enter region q. Enter these limits. This is Alpha 0 for the x one Alpha square root of 4 minus z squared I made a mistake so I gotta go back. Choose number 2. Alpha 0, Alpha square root of 4 minus z squared. Close up the parentheses. That’s better. I say it’s okay. Next one for the y is Alpha 0. Alpha pi. That looks okay. and Alpha 0 for z. Alpha 2. That’s okay. So here’s what you write on your paper. The way you write it with triple integral with dx dz dy order of integration. Here’s the function in here. So you’re going to do the dx first and you put this over here with these lines. Showing you’r doing a range over this integration here. And here’s the integral of the first function okay. And if x equals the upper range. I show quotation marks here but you put you put parentheses in there. Because you’re substituting this amount for an X in the integral. And it equals this, minus sin, etc. And then we do the lower integral. X equals 0 and there’s 0 and you put parentheses around this instead of quotation marks, okay? And here’s the answer, you have the upper range minus the lower range equals this right here. So that becomes the new integration function. And I show you that here. dz dy is left, okay. So now we integrate that. Come up with this. Minus sin, etc. over this range here 0 2. Add z equals 2 Here’s the answer here. And z equals 0. Plug these in for all the Z’s in the problem. And the answer is this. 8, the upper range minus the lower range is 8 sin y divided by 3. Now we’re going to use that for the integration function. With the range of 0 and pi. At y equals pi minus 8 cosine is 8 thirds.

Vectors-Magnitude of A times B

by Leave a Comment

Raw Transcript
Hello, everyone. Tom from everystepcalculus.com and everystepphysics.com. This is an everystepcalculus.com problem. And with my programs. Question on vectors. Let’s get started. Index 8 to get to my menu. Choose A and B vectors. This is a Calculus 3 problem. This student wanted to know how to find the magnitude of A times B. He could get the cross product but he do the magnitude of it. So, let me know you how to do that. You have to enter Alpha before you enter anything into these entry lines, here. So, Alpha minus 2. Alpha one. Alpha one. For the B Vector. Alpha 2, Alpha 1. Alpha 1. So we check see if that’s the vectors that you want. I say it’s okay. A times B is the cross product so we’re going to go to here, A times B. Matrix Multiplication. Write this on your paper, exactly as you see it. There’s the Cartesian System. Notating a vector. Right here. And here’s the answer for the cross product. Zero, four, four. So, we have one vector now which is 0 for X, 4 for Y, and minus four for Z. So now we’re going to go down and we’re gonna find new AB vectors. As we need to put a new vector in for A. So the answer was Alpha zero, Alpha four. That’s for the cross product. Alpha minus four. And we can just quickly go through these because there is no vector for B of A. So now we’re going to go up here and find magnitude of, magnitude of A, number 2. Choose that. This is the way you notate it, it’s got these two lines on the side. It’s called the magnitude of A. Do these calculations. Notice the square root of x square, y squared, z squared and we come up with 5.66 units. Pretty neat, huh? everystepcalculus.com. Have a good one.

Programs Included in Calculus 2 & 3 App

by Leave a Comment

Programs Included in Calculus 2 & 3 App

Raw Transcript

Hello, everyone. This is Tom from everystepcalculus.com and everystepphysics.com. This video is on a menu of Calculus 2 and 3 if you purchased that. What you get. I’m going to go over each item and show you. Index 8 to get to the menu. The busy sign here means that it’s loading the programs. Sometimes it takes longer because of the size of the program but after it’s loaded once, it’s very quick. For instance like this F1 8 to clear, I’m going to press it now. Notice how quickly it comes up right away. I’m going to go up to the top here. And start name the things. Look at this part up here as I name them. A and B vectors, that comes in Calculus 3, generally. You’re doing all sorts of things with adding vectors and subtracting vectors and doing everything possible with them. So A and B vectors, Acceleration, Angle of Vector, Arc Length, that’s the f of x system and then the r t system, Area of a Parallelogram, Component of A Direction of B, Cosine of A and B, that’s the cosine of the A and B vectors. Cross Product, dealing with vectors. Curl computing it at a point, Curl conservative, whether it’s conservative or not, Curl whether it’s divergent, and then the systems of notation which is MNP and PQR for the curl. There’s a double integral, definite integral xy and there’s a definite integral xyz. One is area one is volume. Disk method, Divergence at a point, dot product, double integral, eliminate the parameter, equation of a tangent plane, an equation of a plane, Gradient, Green’s Theorem, Integration by Parts, Interval of Convergence, Line Integral f of xyz, linear approximation 2 variables, linear approximation 3 variables, linear equation, natural log of x the derivative of that, natural log of x the integral, natural log of x solving for x, and then log problems, those are to different bases. Mass and spring of a wire, money, p and q points, parametric equation, partial derivative, partial fractions, partial fraction decomposition, path of objects, polar to rectangle, conversion, position vectors, projection of a on b, projection of b on a, ratio test and series when you’re talking about Taylor and Maclaurin series, rectangular to polar, rectangular box, that’s a standard computation in calculus. Series Convergence, Shell Method, Simpson’s rule, Sine of x cubed, cosine of x squared times. Sketch the graph when you’re talking about p and q points, speed which is the same thing as volume. Sphere center midpoint, Sphere equation, sphere radius, Surface area of Revolution, Surface Integral xy, surface integral xz, surface integral yz. Tangent of log of x, the derivative of that. Natural log of x. Tangent of plane to surface. Taylor and Maclaurin series, Trig and half angled formulas, Trig derivatives and identities, trig integrals, triple integral xyz, triple integral zyx, U Substitution, Unit Tangent Vector, Unit Tangent PQ divided by the magnitude which is PQ. That’s those two lines there on each side of the PQ. Unit Vector Opposite, Vector length, vector between p and q, vector magnitude, Vector, unit, tangent, and Vectors. Which is taking 2 or 3 vectors and finding the angles of those vectors, etc. Quite a series of those. Vector Field Divergent, Velocity, Volume of a parallelpiped, the washer method, and that’s it. Have a good one.

Cross Product A & B Test Question Example-Video

by Leave a Comment

Raw Transcript
Hello, everyone. Tom from everystepcalculus.com and everystepphysics.com. Cross Product with regards to A and B Vectors. It’s a Calculus 3 Vector problem. Let’s do it. Index 8 to get to my menu. We’re going to scroll to Cross Product. Add the vectors. Alpha 8. You have to add Alpha before you enter anything into my menus. Alpha 9, Alpha minus 4. That’s vector A. Vector B is Alpha minus 7, Alpha 8, Alpha minus 3. I always show you what you’ve entered. You can change it if you want. I say it’s okay. We’re going to scroll down to Cross Product. There’s Cross Product. A times B cross product and B times A cross product. Whichever one, they’re different. We’re going to do A times B. And it’s a matrix situation, that’s for sure. So you write these down. Make sure that you keep these in the rows that you have. Make sure you write exactly what you see, here. All these equations. This is I J, and K. That’s a different vector format. 5, 52j, 127k. and here’s the vector situation with the arrows here. 5, 52, 127. Pretty neat, huh? That’s a tough problem if you don’t have a programs, if you don’t know what you’re doing. Especially on a test or something. Go to my site, subscribe so you can see more videos. Have a good one.

Cosine A & B Test Question Example-Video

by Leave a Comment

Raw Transcript
Hello, everyone. Tom from everystepcalculus.com and everystepphysics.com. I’m going to do a problem for Cosine of A & B which is a Calculus 3 problem in Vectors. Let’s do it. Index 8 to get to my menu. There’s cosine of A and B, here. I’m going to add the vectors. Press Alpha first. Alpha 7, enter. Alpha minus 9, enter. Alpha minus 8, enter. Second vector B. Alpha minus 12, Alpha 8, Alpha minus 6. I always show you entered so you can change it if you made a mistake. I say it’s okay. And we’re going to scroll down here to the C’s. And there’s cosine of A and B. Here’s the formula. Dot product of A and B divided by the magnitude of A and the magnitude of B. So here’s the system that you write on your paper. Multiply this times this. And then we’re doing the magnitudes of A which is the square root of all these squares here and same thing with B. You want to try this without the program, go right ahead. It turns to be minus 108 over the square root of 194 times the square root of 244. Square root of 47 thousand. Cosine of minus 1 arc cosine of this here equals approximately 120 degrees, 2.09 radians. Go to my sites, subscribe so you can see more videos, if you want. Have a good one.Have a good one.

Component of A onto B Text Question Example-Video

by Leave a Comment

Raw Transcript
Hello everyone. This is Tom from everystepcalculus.com and that everystepphysics.com. This is a video of Component of A onto B. That’s a vector problem in Calculus 3. Let’s do it. Index eight to get to my menu. Scroll up here. It’s all alphabetical. Component A onto B. If you wanted B onto A, you have to switch the vectors around. So Vector A.. we have to press Alpha before we enter anything in these entry lines here. Alpha 7, Alpha 1, Alpha minus 2. For the B vector, Alpha three, Alpha minus five, Alpha 2. I’ll always show you want you’ve entered. You can change it if you want. Here’s the vectors. These arrows here show that it’s a vector problem. I says it’s okay. And we’re going to scroll down here to. Notice all the things that those two vectors can do. Dot product, cross product. Here’s component A onto B. Here’s the formula. Dot product of A times B times the magnitude of B. So the dot product of A and B is 7 times 3, 1 times minus 5, minus 2 times 2, etc. Total is 12. And of course we have the B where we’ve got the the square root of these squares. They turned out to be 9, 25, and 4. 12 divided by 38, the answer is 6 square root of 38 dived by 19 units. Pretty neat, huh? Go to my site, subscribe so that you can see more videos of me if you want. Have a good one.

Area of Parallelogram Program Test Question Example

by Leave a Comment

Raw Transcript
Hello, everyone. Tom from everystepcalculus.com and everystepphysics.com. Here’s a video on an area of a parallelogram. Okay. This has to do with Calculus 3. Probably with the A and B vectors. So, let’s do it. Index eight it to my menu. I’m already at area a parallelogram. Notice you can scroll down with the cursor, here. And we’re going to add the vectors. You have to press Alpha before you enter anything into these entry lines here. Alpha nine. That’s for X of the A vector. Alpha minus two. Alpha minus twelve. Now the B vector. And the X value would be Alpha 8. Alpha 6, Alpha minus 4. I always show you what you’ve entered. You change it if you want. I say it’s okay. Now we’re going to scroll down here to. This is all you do with those vectors. A plus B, A plus B magnitude. All this stuff that might come up on that test. If there’s a C, I’ll ask you for the C vector also. That’s three vectors. Cross product. Nobody can do a cross product by memory. I certainly couldn’t. Let’s do it again. Let’s scroll down to. There’s area of a parallelogram.Here’s some words right here. You can read all of that. So A times B here we’re doing A times B vectors. And then we’re gonna use that for Matrix Multiplication. The way you set it up. And then you do the various computations. I can’t memorize stuff. That’s the reason that programmed it. But it’s all correct. Mark each one down your paper. Noticed a minus times a minus, you’re always going to screw that up somehow. Look at all the minuses in here. The area equals 80, minus 60, 70 in a vector form. Now you do the square root of the squares of that. It comes up with 122.07 square units. pretty neat, huh? Have a good one.