Double Integral Limits of Integration-Video
Limits at Infinity Test Question-Example 8 Video
Raw Transcript
Hello again, everyone. Tom from everystepcalculus.com and everystepphysics.com A limits at infinity problem. Index eight to get to my menu. You’re going to scroll or get to limits. Choose that. You’re going to choose limit to infinity. You’re going to enter the function by pressing alpha first. You have to do that in every one of my programs. And this is a test from calculus one. One divided by parentheses X minus to infinity. I’ll show you what you’ve entered, you can change it if you want I say it’s okay. We’re dividing it by the greatest power in the denominator. In this case is X. One is the numerator. So one over X is equal to one over X. And when you substitute infinity for X, it becomes zero. Denominator is X over X or three over X equals one or three over X. And 0 divided one, the answer is zero. These are all simple if you really know the trick. If you don’t they can be trouble.
Limit at Infinity Example 1
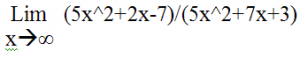
Limit to Infinity Example 2-Solved by TI-89 Video
Lim (7x^3+9(x^2+3)
–> Infinity
Raw Transcript
Hello Everyone, Tom from everystepcalculus.com and everystepphysics.com. I’m going to do another Limit to Infinity problem. Index 88 to my menu. Choose Limits. Scroll to compute limit. Enter the function by pressing alpha. This test problem is seven times x cubed plus nine. Uh oh, I forgot the left parentheses. Press second, go there quick. Divided by x squared plus 3. Add the Infinity indication. Choose the other button, and the yellow register is underneath. See the yellow letters, that’s what that does for us to that register when you press the yellow button there. I always show you what you’ve entered, you can change it if you want. which you better you can change it if want. You’re dividing everything, every term in that problem by the highest order term in the denominator. This here equals this and then we add infinity to these, it’s going to come seven because anytime you take a number. So when you multiply times Infinity it becomes Infinity. So here’s Infinity and second one is zero.Numerator Limit is Infinity. Denominator divided by the highest order term of denominator is this. That equals. When you’re add Infinity, that equals one zero. The Denominator limit is one. The Problem limit is Infinity then. Infinity over one. Pretty neat, huh? everystepcalculus.com, visit my site and buy my programs. Thank you
Limits to Infinity on TI-89 Q4
Lim (7x^3+9)/(x^2+3)
Raw Transcript
Hello Everyone, Tom from everystepcalculus.com and everystepphysics.com. I’m going to show you how to do a Limit at Infinity, on this video. I’m doing several of them so you can get a great idea of what happens.Index 8 to get to my menu. Limits, Choose Compute Limit. Enter the function. Alpha Seven times x cubed plus nine. Oops forgot the other parentheses,
So we press second and the arrow here to get quickly over to the beginning. Add our parentheses and press second and the right arrow to get back where we were. precedent for a second and the right. Divided by parentheses x squared plus three. Need to add the Infinity. Yellow button here.I show you what you’ve entered. You can change it if you want. I say it’s okay. Again, we divide all the terms by the lowest ordered by the lowest quartered term in the denominator. And that equals this for the numerator. And when you do Infinity, the Numerator Limit is Infinity.Denominator…you take those terms and divided by x squared also. Equals one. Infinity divided by one is Infinity.That’s the answer. Problem Limit.
Pretty neat, huh? Visit my site and buy my programs. Thank you
Limits at Infinity on TI-89 Video
Raw Transcript
Hello again from everystepcalculus.com and everystepphysics.com. Another Limit to Infinity problem. Let’s do it. Index 8 to get to my menu. Choose Limits. Choose Compute Limit. Alpha before you enter anything in here. Alpha, parentheses, three times X plus two divided by x.
Add the infinity sign. Alpha yellow button here in the catalog which is the register for infinity. Show you what you’ve entered. I say it’s okay. We take all the terms and divided by the lowest order. X in the denominator, 3 0, the numerator limit is three. Denominator divided by Xis one. Answers is limit is three.
Calculus Q & A-Limits
Question:
Evaluate the limits:
lim(theta symbol–>0-) csc theta symbol
lim(theta–>pi/2) 1/2 tan theta
Calculate this limit at infinity (+/- infinity) for the following function:
f(x) = e^x+e^-x/2
Answer:
When you say f(x), calculus and programmable calculators are saying “y”. When they ask you for a limit, it is a trick question meaning find y. They then give you an x value and say as x approaches 5 (for instance) what is the limit? You then would plug 5 in for x ( which my programs do) and the answer is the limit is the value of “y”. Most of the time they trick you again do to the function they give you which is always a fraction such as (3x+7)/(x^2-4), (always a division sign). Then they ask you as x–>2 (as x approaches 2) what’s the limit. You’ll notice that when you plug in 2 for x you get a zero in the denominator which becomes an “undefined” answer.
If you then (like my program does) add some very small number to 2 such as .001 to get 2 + .001 = 2.001 or take a small number away from 2 to get 2-.001 = 1.999. Setting that equal to x then you actually get a number and that is the limit. I would actually graph the original function quickly on the calculator so I could see the picture of the function and then use the cursor to scroll back and forth at the x value they give you to do things like what happens when x approaches this from the right or left, to give me any clue of what their talking about.
Same thing with infinity. Graph the function first and then logically think about what they are asking. Also start to make things perfectly clear in your calculation examples so there is no question of what you’re asking.
For instance, you have:
f(x) = e^x+e^-x/2 which to a calculator, and me, means
f(x) = e^(x)+e^(-x)/2
and when you mean to say:
f(x) = e^(x)+e^(-x/2)
The problem says calculate the limit at infinity. I would graph the function on the calculator. You can see it’s just a parabola (valley looking, because no minus sign before it).
Here’s what they might be looking for:
f(x) = e^(x)+e^(-x/2)
Convert to:
= x*ln(e)+(-x/2)*ln(e)
factor out the ln(e)
= ln(e)[x+(-x/2)]
ln(e) = 1 So:
(1)[x+(-x/2)]
The limit as x-> ∞
= [ ∞ + (-∞/2)]
= ∞
Limits: Negative Infinity on TI-89 Video
Lim (7x^3+4x-17)/(4x^3-x^2)
Raw Transcript
Hello Everyone, Tom from everystepcalculus.com and everystepphysics.com. A problem regarding limits at Infinity. Index 8 to get to my menu. Scroll down to Limits. You can actually use second to go quicker on the menu, in other words, I want to go up a screen second, and up, second and up,or second and down. And here’s Limits. Click on that. And my other videos that I did previously I didn’t put Limit to Infinity here. You would access it by going to Compute Limit but when you want to put minus Infinity in there. It’s a little bit tricky do that. Well, it’s a little tricky on the Titanium to do that so I decided to put it in a actual menu. So here’s Limit to Infinity. We’re going to put the function in. Press Alpha first. Alpha left parentheses. This is a test problem. 7 times X cubed plus 4 times X minus 17, right parentheses, divided by, left parentheses, 4 times X cubed minus x squared, right parentheses. And let’s go negative infinity. Number two. And there it is there. This is the limit of this with X going to minus infinity. And I always show you if that’s correct. I always give you a change it in my programs. I say it’s okay. Then we’re going to divide all terms by the highest order term in the denominator. Which will be x cubed. Here’s the terms numerator. All divided by x cubed. Here’s the results. Now we put Infinity in for every X. Or minus Infinity, sorry. And that turns out Numerator Limit of 7. These turn out to be 0. Denominator
4 divided by the x cubed. That equals 4. And x squared divided by x cubed equals one over x. We add the minus Infinity to every x.
It turns out to be 40 Denominator Limit. The Problem Limit therefore is seven divided by four or seven fourths. Pretty neat, huh? everystepcalculus.com Go to my site and buy my programs. If you want to pass calculus and/or do your homework. And remember you’ll have these programs for life if you do that.
Limits Infinity Solved TI-89 Video
Raw Transcript
Hello Everyone. Tom from everystepcalculus.com and everystepphysics.com. Limits to Infinity. Let’s get started. Index 8 to get to my menu. Scroll to limits and choose number 2, compute the limit.And the function, you have to press alpha before you enter anything in here. Alpha left parentheses five plus two times X. This appeared on a test. Divided by,left parentheses, 3 minus X right parentheses.
Then press alpha and we press this yellow button here which goes to the letters with the yellow letters about the keys. The yellow register, I call it. And this is infinity right here. Alpha. There’s Infinity. I always show you what you’ve entered. The limit of two times x plus five over 3 minus X, as X approaches infinity. That’s the way you state it. I will show you what you’ve entered, you can
change it if you want. I say it’s okay. You divide all terms by the highest order term in the denominator. And that becomes a minus X
And you take the limited as that approaches infinity and the numerator limit is minus 2.Denominator, you have three and minus x in the denominator and that’s divided by minus x.Three minus x and you take the limit, you put Infinity in here. Anytime you take a number and divide it by Infinity, you get a very large number. It gets smaller and gets closer to zero. So that equals zero. And the other one equals one. That’s the denominator limit. You divide that numerator by the denominator, of course and you get minus two for the problem. Pretty neat, huh? everystepcalculus.com Go to my site and buy my programs.Thank you
Calculus Calculator: Undefined Limit Video
Raw Transcript
This is a video on my programs and how they are applied to the ti89 titanium calculator programs for that calculator today I’m doing a video on limits in particular when a limit is undefined and let’s get started in my main menu you have to get to it by pressing second alpha and press the letters i n d e x then press alpha again put the eight and open and closed parenthesis and then press enter and you’re into my menu there’s many things as you can see in this menu, goes all the way down scrolls all the way up or down parametric equations log of x many many things for you to pass calculus and do your homework right now we’re going to do limits and we scroll to that we have several options under limits table of limits is when they have you on a test put a table down on each side of the approaching point to get the limit I do that too for you to here, but right now were just going to compute a limit and we have to press alpha before we enter any function in my entry lines here in my programs but let’s put the function in for the numerator x cubed minus seven close off the parenthesis divide it by the denominator alway use plenty of parenthesis x squared minus four as x approaches two alpha two I show you what you’ve entered you can change it if you’ve made a mistake but this is x cubed minus seven for the numerator x squared minus four as x approaches two right away I compute the denominator and it turns out to be zero so that makes the function undefined and now our job is to find the limit of that point where it’s undefined so increase the point by one hundredth and put it into your function you put this stuff exactly like you said like it is here on your paper or homework and you’re just substituting that number two point zero one for x in every value of the function and I show you what that computes out to do and you can get an a on this problem the limit is twenty seven point nine pretty neat huh? everystepcalculus.com go to my programs. Enjoy my programs and pass calculus.
Calculus Limits: Table Method Video Example
Raw Transcript
This is a ti 89 titanium program app for with regards to limits and uhm, in some tests there was required to make a table to find the limit of a function and that’s what I’ve programmed here and let’s get started to get to my main menu you have to press second alpha and put in i n d e x the letters and then press alpha again to put in the eight and the open and closed parenthesis and press enter and you’re into my programs i’m already at limits here you can see the number of things here and they keep going way down whatever you need here quadratic formula all kinds of neat things for you to pass calculus or do your homework ah but let’s do limits here and we’re going to do it via the table of limits compute the limit via the table and we’re going to enter our function you have to press alpha to enter anything in the entry lines of my programs so alpha first and then we can enter this here x cubed minus 7 divided by let’s see x squared minus four as x approaches alpha five. I show you what you’ve entered so you can correct it in case you made a mistake I always do that in my programs. I say it’s ok and here’s what you write on your test you have the x side and the y side and you put these values in here and you’ll notice we wanted to get to five here’s five oh one and four ninety nine. So the limit is going to be in between five sixty one and five point six two eight
but you put this on your paper press enter and it will tell you the exact limit which is one eighteen over twenty one If you want it approximately you can divide this out with your calulator pretty neat huh? everystep calculus.com go to my site. Enjoy my programs and pass calculus.
Limits Calculus
Limits in Calculus on the TI-89: Raw Transcript
This is a video on limits as it applies to calculus, generally calculus one, and let’s
get started. You have to press second alpha to get to my menu. You can scroll down from the menu many things you want, all in alphabetical order, we’re going to go down to limits and press enter. Here’s the choices in the limit program you have with regards to limits. You can compute the limit, see the definition of a limit formula, complete a table of limits, and prove that a limit is equal to the computed limit. You can also find delta given epsilon. We’re going to do the first choice now finding delta given epsilon. You have to press alpha before you enter anything in the boxes that come up in my programs. We’re going to try two times x minus five equals one as x approaches three and the epsilon they give you, They will give you these things on the test problem they give you, so epsilon equals point zero one. So I show you what you’ve entered. The limit of two times x minus five equals one, as x approaches 3, while epsilon equals point zero one. The next screen you have the choice of changing it or saying that it is ok. I say it’s ok so I’ll press one for the choice. Here’s the first formula, absolute f of x minus L is less than epsilon. I took the one over here and added it to the minus five to get minus six equals zero. That’s an absolute value sign not a one, and that all is less than point zero one. You’ll keep writing this stuff down on your paper exactly
as it shows. This is the way it done on youtube videos, or at least what I could find, and
delta equals point zero zero fine. Now we can go back to choose main menu or new problem, we want to do a new problem so I’ll choose one again and then go to number two and compute the limit. You can put anything in you want within reason. Alpha again, anytime you are doing division you have to put parenthesis in — in any problem — so we want to make sure we get the parenthesis in there. Let’s go parentheses x minus two closed parentheses, divided by, parenthesis x squared minus x minus two, closed parenthesis. As x goes to alpha two. Here’s the problem you’ve entered and you want to compute the limit. You say it’s ok. Now at x equals two, f of x equals zero and therefore doesn’t exist, so you use the following to find the limit. You add point zero one to every x in the formula so you are a very little away from the limit given and then compute it. The limit is point three, I give you other ways of showing that, because some tests require other answer forms.
Let’s do another problem, let’s do a table of limits — number four — let’s clear
that out and do another one. Alpha closed parenthesis x minus closed parenthesis divided
by x squared minus four, as x approaches two, and here’s the table you’d mark down on
your paper. Let’s do another problem, this is always fun. Prove that the limit is L — the limit
— this is done in always calculus one and throws every student off. Youre panicked because
they are talking about epsilon and delta and the definition of it, which sounds quite complicated, and of course it is useless for the rest of calculus in your life. Let’s put a problem in here. Alpha three times x plus five equals thirty-five as x approaches ten, You have to press alpha again to enter the ten. and here’s what your problem is. Here’s the
formula again. F of x minus L is less than epsilon. You write this stuff down exactly
as shown on your paper. You factor it and then x minus ten is less than epsilon divided
by three. Epsilon becomes delta, and here’s the proof. If zero is less that absolute x
minus c — c is a constant — and is less that delta, then zero is less that absolute
x minus 10 is less than epsilon over three and therefore the original function is less
than epsilon. Put this on your paper and get one hundred percent on that problem. EveryStepCalculus.com check it out and check out the blogs also.