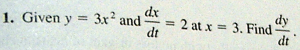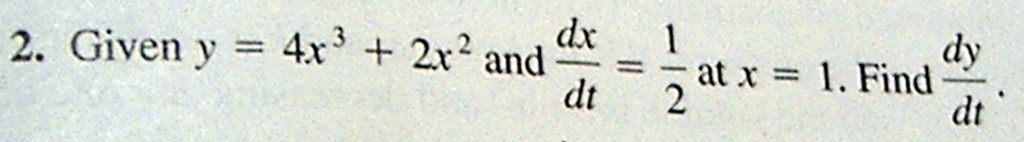Hello again Tom from everystepcalculus.com everystepphysics.com. Related rates problems again regarding a cone or a cone shape, let me read it here one test problem, water is withdrawn from a conical reservoir 8 feet in diameter and 10 feet deep at the constant rate of 5 cubic feet per minute, how fast is the water level falling when the depth of the water in the reservoir is 6 feet? Let’s do it, index 8 to get to my menu then we are going to scroll, related rates is what we are looking for here and then we are going to choose cones number 4 now I haven’t choose the numbers here because I want the screen to be wide enough for you to see the problem properly so I’m just going to scroll down here to cones and what’s given is of course the volume, any time they give you cubic something its volume and then they give you the radius and the height so that’s what we are going to choose and we are finding dh/dt the changing height at a certain level etc. so choose that and have to pressing enter before you press anything in here entry lines alpha 5 feet per minute and its increasing its filling and it shows you what you have enter and you can change it if you want or say okay, the height is given as 10 alpha 10 say it’s okay and the radius is alpha 4 feet I say it’s okay, now we are trying to get rid of; we have r and h and the formula here this is the volume of a cone and we are trying to get so we can get one or the other and this is similar triangle; I don’t know what that means h/r=(10)/(4)=5/2 and so then r is what we use in algebra r=h/5/2 and so now we can substitute that in the formula here for r squared here it is here squared (h) we get (pie)(h) squared/ (75/4) (h) = (h)cubed * (pie)/ (75/4), we are going to differentiate with respect to the volume, time, and height so dV/dt=(h) squared * (pie)/ (25/4)(dh/dt) and they give is a certain height in the problem not radius so we are going to choose that and we are going to alpha 6 is what they give us, say it’s okay so now we are enter that in the (h) squared here (pie)/ (25/4)(dh/dt) =(18.1)(dh/dt) and we use the algebra (5.)/ (18.1) is dh/dt = .27631 (ft)/mn. Pretty neat ah, every step calculus.com go on my sight buy my programs you are going to enjoy them and you’ll have them for life in your calculator, you will throw your book away but you will never throw away your calculator with my programs because you can do it for your grandkids, your partner, your spouse and who ever in the future, somebody is going to run in calculus again in the future.
Calculus Rate of Change | Mans Shadow Problem
A man 5 feet tall walks at a rate 5 feet per second away from a light that is 16 feet above the ground. When he is 8 feet from the base of the light, find the rate at which the tip of his shadow is moving.
Raw Transcript
everystepcalculus.com. Related Rates problem concerning a shadow of a man and a light pole. Index 8 to get to my menu. We’re going to scroll down to Related Rates, here. Here’s related rates there. Then we’re going to scroll down to shadow. Lamp post, person, shadow changing. Here’s a picture of it. And the lamp post is given as Alpha 16 feet high. You have to press Alpha before you enter anything into these entry lines, here. A mans rate of change is Alpha 5 and it is increasing because he is walking away from the lamppost. And the mans height is alpha 5 feet, the distance given is alpha 8. I always show you what you’ve entered, you can change it if you want. I say it’s okay. I show you the definitions of what we’re talking about. Now we do the calculations. You write all this on your paper, of course. Exactly as you see it. And so the change of is 88 over 11 feet per second. Now you can work this out if you want to, you know with a calculator. 88 divided by 11, this is the exact answer. And the second part of the problem. What’s the length of the shadow changing? And you do this calculation here. It turns out to be 25 over 11 feet per second. And you can do the approximation if you want on your calculator. Have a good one.
Related Rates – Pulley Rope
A boat is being a pulled into a dock by a rope attached to it and passing through a pulley on the dock positioned 8 feet higher than the boat. If the rope is being pulled in at a rate of 2 meters per second, how fast is the boat approaching the dock when it is 9 meters from the dock?
Raw Transcript
Hello, everystepcalculus.com, a problem in calculus with related rates: a boat being pulled up to a dock, where the dock is higher than the boat problem. Let’s do it, you can see the problem on your screen. Index 8 to get to the menu, we gotta go up to… gonna go up on the cursor so we can go to the bottom of the alphabet to get to the R’s quicker. This is calculus 1 but also it’s in calculus one, two, and three. Related rates and we’re choosing the “Boat/Dock pull”, number 2, and we’re gonna enter our parameters. We have to press alpha before we enter anything into these entry lines here. Alpha, the height is given as alpha 8 meters, the ropes rate of change is equal to alpha 2 meters per second, it’s decreasing because it’s going closer to the Y axes. It’s pulled in, enter distance from the dock is alpha 9 meters. I always show you what you’ve entered, you can change it if you want. I say it’s okay, and I give you the perimeters, now what we’re talking about here, x equals distance from the boat from the dock and y equals the height of the dock above the boat, and L equals the length of the rope, which is the hypotenuse. And of course dL/dt is the rate of change of minus two meters per second. Given. So we find the length of the rope, which is equal to the square root of 145. Pythagorean theorem. And then we formulate the same equation basically but we work out a little bit different because we’re gonna do the derivatives of everything here. So um we do the derivatives you read all this on your paper, you do all the derivatives of the whole function before, just like this, and that’s the answer. Really the answer is square root of 145 times a minus 2 divided by 9, which is dx/dt which is the change of rate of the x axis as the boat is being pulled up the dock. And the approximate answer is -2.6759 meters per second. Have a good one.
Using Calculus for Rate of Change | Lamp Post & Shadow
Raw Transcripts
everystepcalculus.com A related rates problem concerning a shadow of a man and a light pole. Index 8 to get to my menu. We’re going to scroll down to related rates, here.
There’s related rates there there. We’re gonna scroll down here to shadow. Lamp post,person, shadow changing. Here’s a picture of it. And the lamp posts is given as alpha 16 feet high. You have to press alpha before you enter anything into these entry lines, here.
The man’s rate of change is alpha five and it is increasing as he’s walking away from the lamp post And the mans height is alpha five feet. The distance given is alpha 8. We show you what you’ve entered, you can change it if you want I say it’s okay. I show you the definitions that what we’re talking about. And we do with the calculations. You write all this on your paper, of course. Exactly as you see it, of course. And so the change is 88 over eleven feet per second. Now you can work this out if you want to you know your calculator. 88 divided by 11. This is the exact answer. And the second part of the problem What’s the length of the shadow changing? You do this calculations here. It turns out to be 25 over eleven feet per second. And you can do the approximation if you want on your calculator. Have a good one.
Related Rates with TI-89: Triangle Heated
The area of an equilateral plate, being heated, is increasing at a rate of 150 mm²/min. At what rate is the length of a side changing when the sides are 250 mm long?
Raw Transcript
Hello everyone. Tom from everystepcalculus.com and everystepphysics.com I’m going to do a test problem on an equilateral triangle with regards to related rates. Let’s see the problem is the area of an equilateral triangle plate being impeded is increasing at a rate 150 millimeters squared per minute. At what rate is the length of a side changing when the sides are 250 millimeters long? So, let’s do this. You have to put in index 8 open and close parentheses to get to my menu. And we’re going to scroll down to average rate of change. You could scroll to related rates. Let’s do that. They are both the same. And scroll down to the R section here. Here’s Related Rates there. And we’re going to hit number 7 for Equilateral Triangles. I’ll show you the formula here. Write this stuff on your paper. And of course you differentiate both sides with respect to time. What’s given here, they’re giving you the rate of change of the area so we’re going to go and enter the change. I’m going to press alpha to put anything in here. Alpha 150. And it gives millimeters. Choose number 2. And it gives minutes. Choose number 2. And then the side is Alpha 250. Now we’ll show you what you’ve entered so you can change it if you want. Say it’s okay. Write all this down.
Exactly as you see it. Here’s an answer. .69282 millimeters per minute. Pretty neat, huh.
everystepcalculus.com. Go to my site, buy my programs, and subscribe to me so that can see other videos
Related Rates Test: Ladder Against Wall Video
Related Rates Test: Ladder Against Wall Video
Raw Transcript
Hello. Tom from everystepcalculus.com
Related Rates. These are word problems. Very difficult
even though seemingly simple but
let’s get started. Index eight is calculus one in my program to get to my menu.
That comes with my instructions of course and we’re going to scroll down to
from the menu on a scroll down to related rates. Could be on a test
homework or something and we find it all alphabetical
and in this case
we’re gonna do a ladder against the wall which is the usual
calculus problem related race
problem. It’s used in the Kahn Academy
for their example and also in this example here
from number nineteen. So when I scroll down to that
and we’re going to press enter.
I show you what it looks like. Here’s the ladder
and here of course is the y axis and the x axis. All related rates
are right triangle basically. And they
I ask for them at ladder length. You have to press alpha before you enter anything in
the my entry lines in my programs
and they give it as five meters.
And then you have to decide which is changing.
Is the ladder moving down the y axis
or is the bottom moving? Do they give you the bottom moving right or left?
So, in this case is the y is
the ladder is moving down to give you that change.
So we’re going to choose number two here.
Press Alpha again and they give that to you
as one meters per second so we’re going to choose one. Press enter.
And then they give you
certain distance on the x axis so we’re going to
press and that you need to use three. So we have these
parameters given. I ask you if that’s correct.
You can change it if you want. I say it’s okay.
The first thing with these ladder problems is that you have to find out the other side so
of course x squared plus y squared equals z squared and the
one that we don’t know is the y. We know the x is three and we know the
ladder is 5 so we need to figure that out.
So we do that automatically for you here.
It’s 4 units. I say units because they may be centimeters it, it might give you millimeters, it might give you something else.
You decide yourself and put those in for units.
In this case are getting in meters.
And then they the use implicit differentiation to
to differentiate these
terms here and so we have to do the derivative
of x squared, the derivative of y squared with respect to T
and T is time. The x axis is actually time also.
and z squared. We know z squared is 5 so you write all
this on your paper.
and it turns out to be a -1.33 units per second.
Pretty neat. everystepcalculus.com Go to my site, buy my programs and subscribe
to me also so you can see future
movies and blog.
Related Rates Video on TI-89: Square Area Increasing
Related Rates Video on TI-89: Square Area Increasing
Raw Transcript
Hello everyone Tom from every step calculus dot com.
Related rates problem.
Right off of Yahoo on the Internet.
Where they ask the questions and
a lot of them try to answer it. Let’s get started, index8() to go to my menu.
And
going to, all the instructions come with my programs of course how to do all this
stuff. We’re going to,
go down to related rates.
Scroll down related rates because that’s the problem
we’re doing.
Here we are here, and we
these are all alphabetical everything is you wanna get to
this problem involving a square the area of a
square. So we’re gonna go down, that choice on the menu.
And
related rates always deals with a formula and then
changes that to derivatives with respect to time.
And so you write all this down area equals s squared.
I give you this little hint, s equals a side and we’re gonna find
da/dt the how the area is changing
with regard to time. And so
now we’re gonna do the calculation here’s the a equals s squared where there’s a
formula and we do the derivative
left side derivative of the right side with respect to T
time. And that turns into
the derivative of area with respect to time and then we have
derivative of s squared which is 2s.
And then ds/dt. This problem they give you area so we’re gonna choose that.
Otherwise they might give you side.
You try to make all those choices for you.
You have to press alpha before you enter anything in these entry lines. I’m gonna press alpha
give you 64
as the area.
I always show you in case you made a mistake I say it’s okay.
and of course the square root of the area is the side.
The formula is inside so we have to change it to that, so that’s 8
And then they give you centimeters.
They might give you any these. And the side is increasing at alpha,
8 centimeters per second
Again I show you its
8 centimeters for the side and 8 centimeters per second for the
change in the side which is ds/dt with regard to time.
Ok, so here’s the
answer you do the problem,you insert variables
Here’s the formula what we found before you insert the variables and you come up with this
answer.
Pretty neat huh? every step calculus dot com You can go to my site buy my program
pass your calculus test and maybe subscribe to me also
on the site so that
you can see my future movies and blog.
Related Rates Video: Square Area Heated
Related Rates Video: Square Area Heated
Raw Transcript
Hello everyone, Tom from everystepcalculus.com, we are going to do related rates versus a square and the area how it increases the feet, letís get started.
Index 8 to go to my menu and since its related rates average rate of change is the same as related rates, Iím going to press 2 here and wait for it to load here for a second and weíre going to scroll down because when you have an arrow like this it shows you thereís more in the menu and itís all alphabetical, so we want to get square area, this is problem number 7 book and so we want to do that, we want to show you how itís done. Related rates always deals with the calculus formula of theyíre dealing with and then you differentiate that on both sides with respect to time and weíre asked to find the change in area which is the derivative of A versus change in time and here is the actual formula for area and you write this all in your paper, this is exactly what you should write and theyíve given us the side in this problem number 7, so you have to put in, first you have to press alpha before you enter anything into these entry lines here. Alpha 12 is given, centimeters and the side is increasing, so they give you alpha .08 and thatís per minute instead of seconds, I gave that choice in my program, itís pretty neat there. So you have 12 centimeters per side and you have ds/dt which is the change of the side with respect to time .08 cm/mn, Iíd always give you a chance to change your in case you made a mistake, Ok and here is the answer. Pretty simple but remember you can do these problems for the rest of your life if you get these programs, if you get my programs versus if you just memorize it now and forget it later, so everystepcalculuc.com, go to my site, buy my program, pass your calculus class and also subscribe to me so you can see other videos and blog.
Related Rates: Given dx/dt find dy/dt
Related Rates Test Question: Given dx/dt find dy/dt on the TI-89
Raw Transcript
Hello Tom from every step calculus dot com.
We’re going to do another related rates problem with a function this time.
Uh, put index8() into here to get Calc one menu.
And we’re going to scroll scroll up
get to the bottom of the alphabet here. We need to get to related rates
which is what we’re doing. And we’re going to choose number three because
we’re going to do a function.
Gonna enter the function we have to press alpha before you enter anything into my
entry lines here. And y
in this problem.
Is alpha three times
x squared.
I always show you what you’ve entered so you can change it.
If you made a mistake. And they’re asking in this problem
for dy/dt. We’re gonna choose number one here.
And we’re gonna enter what the problem is, which is.
dx/dt is 2. And
X equals three, alpha 3.
I say it’s okay.
And here’s the
answer ,36 units.
Pretty neat huh? Every step calculus dot com. Go to my site buy my programs and subscribe
to me
for future movies.
Also if you have a related rates problem that you, that’s
not in my programs if you want me to do you can always contact me
and I’ll set it up for you.
Related Rates Video: Sphere Expanding
Related Rates Video: Sphere Expanding
Raw Transcript
Hello everyone this is Tom from every step calculus dot com.
Going to do a related rates problem
with concerning a sphere. And
let’s get started. You put index8() into the entry line here to get to my
menu.
And we’re going to scroll down to
related rates. You can hold the scroll button down like I’m doing here
go down, keep going down. Until we get to the
the r section.
Here we are related rates. And we’re looking for a sphere.
You know we can go up with the cursor to get to the bottom of the menu. Cuz were
alphabetical here. Here’s sphere volume. There’s the formula right that on your
paper. You get two points for that right away.
And we’re gonna find,
we’re finding the rate of the radius.
dr/dt with respect to time. And the inflation rate would be
alpha, you have to press alpha before you enter anything in these entry lines here.
Alpha 4.5 and its increasing,
you press number two. And is concerned with minutes.
And then what’s given is the
radius. Press two on that.
And what we get is two-inches.
Alpha 2 inches.
Number four. I’ll show you what you’ve entered you can
change it if you want. Here’s cubic inches for minute. I say it’s okay
and here’s the process.
dv/dt is equal to 4/3 pi
three r squared et cetera et cetera. Write that on your paper,
and here’s the answer .08952
inches per minute. Pretty neat huh? EveryStepCalculus.com
Related Rates TI-89 Video: Circular Plate Heated
Related Rates Test Question: Circular Plate Heated
Raw Transcript
Hello everyone Tom from EveryStepCalculus.com.
A related rates problem, number
8 in my book, calculus book. let’s do it.
index(8) to get to my menu. Average rate of
change is the same as related rates in my thinking.
I’m not a professor. And we want to do
in this problem number 8 is something to do with the circle.
So we’re gonna go, and the area, we’re gonna do Circle area here.
And here’s the,
related rates you always deal with a formula. And differentiate both sides with respect to T. So
here’s the formula for the area of a circle pie r squared.
And they give you radius in this problem they could give you diameter. I changed
that, I
try to catch everything that these professors try to trick you with.
And everything in physics and calculus is a trick,
memorization and tricks.
Enter radius given, okay we have to press alpha before we enter anything in
this
entry line here and my programs. And they give us at five centimeters.
I’ll take you through it and we’re asked to find the
change in area, that’s dA/dt with respect to time.
And we’re going to enter the rate,
rate they gave you, they always give you the rate of something.
And so we press alpha, and put in here .2
and its increasing.
And it’s per hours so we’re gonna choose number three.
So here we have dr/dt which is the radius which is
changing at .2 centimeters per hour. And the radius is five centimeters.
You change it if you want I always give you that option.
In case you made a mistake. And here’s what we’re doing with differentiating
left side area with the right side. And we come up with this 2 pie r dr/dt.
We add the variables right here which I show you.
calculation is 6.28 centimeters squared per hour.
Pretty neat huh? EveryStepCalculus.com Go to my site buy my programs
and pass calculus class.
And you’ll have these programs for the rest of your life your kids or grandkids or
yourself or neighbor or whoever. If you don’t then you
just memorize and forget like all college kids do.
Um so anyways go to my site
buy my program and pass calculus test but then maybe even
subscribe to me so you can catch other videos I make
or a blog here and there.
Related Rates TI-89: Airplanes in Flight
Related Rates TI-89: Airplanes in Flight
Related Rates Test Question: Two airplanes pass each other in flight at 9:00 AM.
One is traveling East at 90 mi/h. The other is traveling South at 180 mi/h. How fast are they
separating at 11:00 AM?
Raw Transcript
Hello Tom from every step calculus dot com.
Going to do related rates problem. Let’s get started.
index8() in the entry line here to get to my menu.
Press Enter. We need
related rates are we could get average average rate of change.
Both the same.
And we’re gonna do in this problem this is two airplanes passing each other.
At a certain time. And
what’s their rate of change as they separate. And
in these kind of problems we’re gonna, we’re gonna go to north, south, east or west.
In the menu which is number 8.
You can scroll down with the curser or you can press the number before it.
I press number. And
were going to do the problem. The most important part of north and south
is this pathagorum theorem type thing which is,
and then the derivatives of that. Your
implicitly differentiating
both sides of the equation to come up with the most important part. Here’s the
thing if you can figure out
(x) and dx/dt.
(y) and dy/dt and your gonna get
dz/dt which is most the time what they ask for.
Which is the hypotenuse of a right triangle.
So make sure you mark this down on your paper.
Here’s how you got it.
Of course the 2’s are cancelled, I put this here.
They always give you time. So in this,
in this problem they give 9:00 am so we’re gonna press number two to go to a.
And we’re going to push alpha, to push
alpha before you enter anything in these entry lines here.
alpha 9 a.m. and the other one is
a.m. also so I’m going to press to 2 here. And put in alpha
11. I will show you what you’ve
entered, so you can change it if it’s a mistake, 9 AM and 11.
And of course that’s two hours elapsed time
in between this flight here. And we’re going to enter the speed of the
first plane which is
Alpha
0:00
Miles per hour we’re going to choose number 3. And the direction here is East. We’re going
to choose number three again.
And then we have the other plane which is
alpha 180
And that’s going south, we’ll press number 4.
The miles per hour will be the same for both. It will be the same.
So here again I show you’ve entered you can change it if you want.
I say it’s okay. And
the first thing you do is find out X with respect to time.
So about 90 miles per hour.
And about two hours it’s 180 miles per hour.
You write this down on your paper, there’s a system for doing these problems.
on related rates. Then we need to know the hypotenuse
that’s the pathagorum theorem. So we do it here, you write this on your paper
that’s 402 miles per hour, that’s the hypotenuse.
And you plug these factors in X 180 dx/dt
was 90 and here’s 360.
And dy/dt was 180, divided by 402
which is, and this is the formula here.
(x) dx/dt plus y dy/dt
divided by z equals dz/dt which is they’re asking for. So 201
miles per hour. 100 percent on this problem on
your test. EveryStepCalculus.com go to my site buy my program pass your calculus test.
I promise you and also subscribe to me if you wanna see
future videos or blog.
Related Rates: Change in Cube’s Heat & Volume
Related Rates: Change in Cube’s Heat & Volume on TI-89
Raw Transcript
Hello everybody, Tom from EveryStepCalculus.com
I’m gonna do a related rates problem again, um and relationship to a cube.
Remember related rates always have some sort of formula to differentiate on both sides and come up with their answers. And let’s get started. index8()
to go to calculus one menu press ENTER here
you sometimes they call it average rate of change
or related rates in test
you can scroll on that one right I’m going to scroll down to
related rates there’s related rates there
I give you a list of things
keep adding to it in this case we want a cube is heated in the problem that
I’m showing here. And so we’re going to choose that
because it says a cube is heated your going to go to here
and related rates here find the rate of change in the volume
of a cube due to heating and of course here’s the formula
for the volume of a cube sided cubed
s = side and
they give you what the side
is. You have to press Alpha before we enter anything in my entry lines here.
And they give it is 12. Now they might
give you inches, feet, meters or centimeters. In this case they give you centimeters.
So I give you that choice. And then they give you the,
what’s changing with regard to heat. You have to press
Alpha. In this case they get .1. And of course they have seconds, minutes or
hours depending upon what the problem gives you. In this case they give you minutes, I’m going to Press 2.
I always show you what you’ve entered, so you can change it if you want.
Here’s 12 centimeters and .1 centimeters per minute.
I ask if it’s OK.
Here’s the answer 43.2 centimeters cubed per minute.
And, notice that your differentiating the v, volume.
And differentiating the formula
which is side cubed.
And that becomes dv/dt differentiating V.
And then we’re, we add our
derivative.
S cubed is equal to 3 S squared.
dS/dt we’re taking the derivative of
side with respect to time. And here’s three times 12
squared. And then we add the change of
rates. These are pretty easy but why not, even if they are easy, why not do it
with the program. Just so you do it within 10 seconds and be done with the problem
on a test. Then go onto something else. You can memorize it
and do it if you want. This is much better
EveryStepCalculus.com go to my site buy my programs and pass calculus. And
don’t forget to subscribe to me for different videos and blog.
Related Rates | Spheres Radius & Volume | Every Step Calculus
Related Rates | Spheres Radius & Volume Test Question
Raw Transcript
Hello everybody this Is
Tom from EveryStepCalculus.com I’m gonna do a related rates
problem right off the internet and this
problem was the first when i searched
related rates for a sphere and related rates is always got some sort of formula
to it they deal with cones and
spheres and cylinders and
this one is a sphere so we’re going to get started index eight to go to my
calculus one menu and we’re gonna
you can go up or down on this, this scroll up there down by like to go up
if the
the letters are r there related rates which is closer it z than a
and wait for it to load here
and you can see this
arrow here and on any menu shows you that there’s more to it than that
they’re all in alphabetical order so sphere would be
in the s section here’s sphere
and in the problem that
was on the youtube your asked to find
dv/dt in other words how much is the volume changing
with the change in radius and so we’re going to choose number two
to do that and the radius rate that they give you
is 4 so we to enter anything into these entry lines on my program any of my
programs you have to press alpha
first alpha 4 and
the problem says its increasing we’re going to choose number two you can scroll to it
here or you can choose a number before it
I like to choose the number it’s quicker and it says per second we’re going to choose
that
and then it gives a diameter
so the radius but the formula is with radius so that needs to be converted
you give you a diameter the little tricks in calculus or physics they love the trick
you
and so the diameter is alpha
he gives an alpha of 80 and which is the radius of 40
divided by 2 and he gives millimeters
notice how many variables there are in this problem in other words millimeters
per second um, the
related rate for the radius and
change in volume so you you got many
things this one he gives millimeters
so we’re going to choose that I show you what you entered so you can change it if you want notice
millimeters cubed per second and the radius is millimeters then
have to be the same I say it’s okay
you write this all on your paper here’s the computation of the actual formula
within related rates in other words we’re taking the derivative
verses with respect to time to
of both sides of the equation there’s
v and here’s the right side and that turns into
4 pie r squared dr/dt then you add the variables here
and what comes up is 25600 pie
millimeters cubed per second now notice that
you would get 100% on this problem but if you had minutes you would have been
wrong if you had feet you’d be wrong et cetera so
the program catches all this stuff so you get a 100%
fabulous program one of the best I’ve written
go to my site
buy my program to pass calculus and if you want you can subscribe to me also
and
see future movies and enjoy my programs as I show them
and also a blog
Related Rates Test Q: Function dy/dt on TI-89
Related Rates Test: Function dy/dt on TI-89
Raw Transcript
Hello gang Tom from EveryStepCalculus.com
gonna do a related rates problem again
Gonna do a little bit more difficult function let’s get started index eight to get to my
menu
and scroll up to get the bottom
r is closer to z than it is to a then you want related rates, there it is
and we’re doing a function so we’re going to choose number three
We’re going to enter our function press alpha
4 times x
cubed
plus 2 times x
squared
Now we show you what you have entered you can change it think you made a mistake and they’re asking in this
problem
number two for dy/dt
we’re gonna choose number one here and they give you alpha
1/2 going to put in
you can put 1/2 I’m going to put in point 5 here
and that x equals
and so we go alpha 1
and I show you in case you want to change it and here’s the
what you marked down on your sheet
you’ve got 8 units here. Pretty neat huh? EveryStepCalculus.com
go to my site buy my programs pass calculus
class also subscribe to me if you feel like it
future movies and blog you have a problem in
related rates you can
email me that and I’ll program it for you here
Related Rates Test: North-South-East-West Rate of Change
Related Rates Test: North-South-East-West Rate of Change on TI-89
Raw Transcript
hello everyone Tom from every step calculus dot com
uh, gonna do a related rates problem
with north and south and east and west type of problems that
occur on tests, and planes going north and going east and
what’s their rate of change etcetera and
we’re gonna do a number 6
in this example put index eight in here to get the calculus one
menu and we’re gonna scroll up to get to the bottom of the menu and get two related
rates
press Enter
and we’re gonna do
north south east or west number 4 here press 4 or you can scroll to it like with
the cursor here
or you can just press the number before
you write this on your paper x
squared plus y squared equals z squared we’re going to do the derivatives of each one
d/dt of x squared plus y squared on this side of the problem
and z on the other side here’s what you get
you get 2x..derivative of x squared is 2x
etcetera derivative
of y squared is 2y respect of t which is time
and same thing with 2z the 2’s go out
you can divide through by 2 and so you get this right here
write all this on your paper just exactly as you see it nothing left out
the only things that
dx/dt is given that means that the x axis
horizontal is what their after
let’s see, a man begins walking
due North so due North is the y so
it wouldn’t be that one, so the woman is walking east
which is on the x axis
so were gonna do alpha always press alpha
before you enter anything in these entry lines here alpha 4
and then the Y
the man is going north so he is going alpha 3
and after time of one hour what’s happening alpha
1, show you what you’ve entered so you can change in case you made a mistake, it’s
okay
write this on your paper x is dx/dt over t is at 4 over 1
your entering all the variables here
x equals 4 y equals three
and then we can do
the pathagoram Theorem all this is easy if you know it but I mean on a test
even if you do know it is nice to do a problem quickly and be done with it
and get 100% on it and move on to something else so Z equals five
so that’s the answer 5 miles per hour
make sure you write all this on your paper
every step calculus dot com
goto my site buy my programs pass your calculus class and also subscribe to me if you
feel like it
for a future blog or movies if you have a
related rates problem you can send it to me and I’ll program it here
right for you
Related Rates: Current & Resistance on TI-89
Related Rates: Current & Resistance
Raw Transcript
Hello this is Tom for every step calculus dot com
I’m gonna show you how to do related rates now which is a
pretty technical problem unless you
study it all day and really know it is pretty simple with my programs
this is a actual test problem
On related rates regarding current
and resistance so
let’s get started put index8() here to get my menu
you can go up on the screen to go down to
lower alphabet these are all..I’m going to choose related rates here
and here’s the formula for
voltage, resistance and current v=ir
and they always give you the
voltage change here which is alpha, you have to press alpha
before you enter anything in the my entry lines here and alpha 3
and sometimes they have an increasing or decreasing
I let you choose that, it says decreasing and the volts are alpha 12
and the current is
alpha 48
I always show you what you have entered
you can change it if you want say it’s okay first of all we do the formula to
find out what the resistance is
given the voltage and current and then you write all this down
on your paper, d/dt, your doing, your taking the derivative
of the voltage and the derivative of right side of the equation, i and r
this is the product rule now because remember you got a times sign in-between here
and that’s always the current times the
derivative of the resistance and resistance times the derivative of the
current with regard
to time and then we do the
we plug in the variables all automatic here
here’s the answer .01563
ohms per second, pretty neat huh? every step calculus dot com
goto my programs goto my site and buy my programs and also
maybe subscribe to me and my
sites you can see future blog
or future movies
Average Rate of Change Calculus Video | Step by Step on the TI-89
Raw Transcript
This is a video from everystepcalculus.com demonstrating how my programs work on a TI-89 Titanium calculator and other calculators in the TI system for physics and calculus problems. This is a problem on average rate of change in calculus a problem that comes up in tests and professors talking about it. So let’s get started in my programs you have to push second alpha to put in the letters i n d e x and then press alph to put the eight and the open and closed parenthesis. press enter and you’re into my menu the first one is average rate of change because it’s got the a in it alphabetically we’re going to scroll to that press enter. This is a problem that might be on a test I give you some sort of definition average rate of change the amount of change in one item divided by the corresponding amount of change in another we’re gonna enter the function we’ll enter the one up here a little more elaborate let’s go. You have to press alpha before you enter anything in my entry lines here let’s go three times x squared plus six times x minus sixteen I always show you what you’ve entered so you can change it in case you made a mistake I say it’s ok and you have to have a range so we’re gonna give the range of a or b lower range, let’s go alpha eight and the upper range. Let’s go alpha eleven again I show you what you’ve entered here’s the formula for it f of x sub two minus f of x sub one divided by x two minus x one I’ve put the variables in there for you so you write this on your paper this is what you’d write on your test paper or homework right away, so you don’t think about it do what ever comes up on these screens notice I’m substituting eleven for all the x’s in this function that comes to four thirteen eleven the upper range here’s the lower range eight substituting eight for every thing you write this all on your paper here comes the answers. Now we plug it into the formula and the average rate of change is sixty three what does this mean this is the slope of a line sixty three over one rise over run you go up sixty three points on the y axis go over one on the x axis draw a line from that through the origin of the graph and that’s what you found the slope of a line. Congratulations. Pretty neat huh? everystepcalculus.com go to my site. Buy my programs and pass calculus.