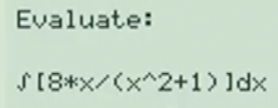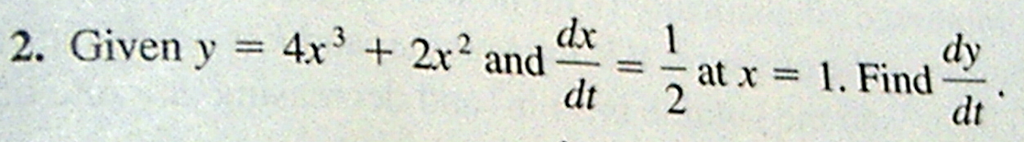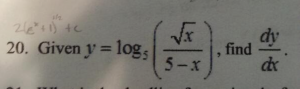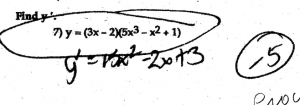Related Rates Video: Sphere Expanding
Raw Transcript
Hello everyone this is Tom from every step calculus dot com.
Going to do a related rates problem
with concerning a sphere. And
let’s get started. You put index8() into the entry line here to get to my
menu.
And we’re going to scroll down to
related rates. You can hold the scroll button down like I’m doing here
go down, keep going down. Until we get to the
the r section.
Here we are related rates. And we’re looking for a sphere.
You know we can go up with the cursor to get to the bottom of the menu. Cuz were
alphabetical here. Here’s sphere volume. There’s the formula right that on your
paper. You get two points for that right away.
And we’re gonna find,
we’re finding the rate of the radius.
dr/dt with respect to time. And the inflation rate would be
alpha, you have to press alpha before you enter anything in these entry lines here.
Alpha 4.5 and its increasing,
you press number two. And is concerned with minutes.
And then what’s given is the
radius. Press two on that.
And what we get is two-inches.
Alpha 2 inches.
Number four. I’ll show you what you’ve entered you can
change it if you want. Here’s cubic inches for minute. I say it’s okay
and here’s the process.
dv/dt is equal to 4/3 pi
three r squared et cetera et cetera. Write that on your paper,
and here’s the answer .08952
inches per minute. Pretty neat huh? EveryStepCalculus.com