Raw Transcript
Critical Points-Work Shown on TI-89-Video
Transcripts
Hello, Tom from everystepcalculus.com,and everystepphysics.com. A problem in calculus dealing with critical numbers in critical points of a function. Let’s do it. Index 8 to get to my menu. Then your going to scroll down to critical point or numbers.I always have you start a graph on your paper. When you enter the function you have to press Alpha before you enter anything into these entry lines. Your going to press Alpha X cubed minus 3 times X. I always show you what you’ve entered. You can change it if you want. I say it’s okay. And we’re gonna choose number five, critical points.
Triple Integral: Work Shown on TI89-Video
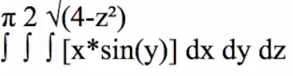
Transcripts
Hello again, everyone. This is Tom from everystepcalculus.com and everystepphysics.com. I’m going to do a Triple Integral for Calculus 3 right now. This is an example of a Patrick JMT, my favorite instructor on the internet, on YouTube. So I’m going to show you how it works on my program. I don’t know anybody can do that problem. He can do it because he’s a genius. But for us students,etc. How do we do it? Let’s get started. Index 8 to get to my menu. I’m going to scroll up because I can go to the bottom of the menu then instead of going down quicker to go to the T’s section. And we’re going to choose Triple Integral. And we’re going to enter our function. You have to press Alpha before you enter anything into these entry lines here in programs, okay. Alpha x times sin of Y. I always show you what you’ve entered. You can change it if you want. And we’re going to use the order of integration which is dx, dz, dy which is in the example. You have the other choices in case that’s given on test also. And we’re going to enter region q. Enter these limits. This is Alpha 0 for the x one Alpha square root of 4 minus z squared I made a mistake so I gotta go back. Choose number 2. Alpha 0, Alpha square root of 4 minus z squared. Close up the parentheses. That’s better. I say it’s okay. Next one for the y is Alpha 0. Alpha pi. That looks okay. and Alpha 0 for z. Alpha 2. That’s okay. So here’s what you write on your paper. The way you write it with triple integral with dx dz dy order of integration. Here’s the function in here. So you’re going to do the dx first and you put this over here with these lines. Showing you’r doing a range over this integration here. And here’s the integral of the first function okay. And if x equals the upper range. I show quotation marks here but you put you put parentheses in there. Because you’re substituting this amount for an X in the integral. And it equals this, minus sin, etc. And then we do the lower integral. X equals 0 and there’s 0 and you put parentheses around this instead of quotation marks, okay? And here’s the answer, you have the upper range minus the lower range equals this right here. So that becomes the new integration function. And I show you that here. dz dy is left, okay. So now we integrate that. Come up with this. Minus sin, etc. over this range here 0 2. Add z equals 2 Here’s the answer here. And z equals 0. Plug these in for all the Z’s in the problem. And the answer is this. 8, the upper range minus the lower range is 8 sin y divided by 3. Now we’re going to use that for the integration function. With the range of 0 and pi. At y equals pi minus 8 cosine is 8 thirds.
Find the Gradient of Point-Video
Gradient Solver at Point (1,2) Video
Magnitude of a Vector P&Q Points-Video
Equation of a Plane Using 3 Points-Video
Solving Equation of Plane 2 Points-Video
Eliminate the Parameter XYZ Plane-Video
Divergance at a Point Curl Solver-Video
Disk Method Revolving Around Y Axis- Video
Disk Method Solver-Video
Solving Definite and Indefinite Integrals – Q&A
Dear Tom,
I would like to know if your program also solves integrals consisting only of symbols like x, a or b in both definite and indefinite matters?
Example:
![]()
or
![]()
Would solving does definite integrals be possible using your programs showing the solution process step by step?
Kind regards,
Ben
Answer
The first integral, sounds like your professor didn’t teach you, so you will want my programs to teach you or me to teach you. A common endeavor in my experience. When you see the da that’s “with respect to” in other words, you are integrating that integral with respect to “a”. In my programs you’d change all the “a’s” to x”s.
Now could you solve the integral if it looked like:
x x
∫ (1/x)dx or ∫ ( 1/[(c+b)-(k+x)] ) dx
o o
Now these would never appear on a test unless your professor demonstrated them on the black board, so they are either homework or experimenting off the internet. Both integrals are definite integrals because they show a range to integrate over. When you solve the integrals you have the area under that functions curve. That’s all integrals do is solve area under curves. You can graph 1/x on your calculator and you can see what the first integrals function looks like. Now, anytime you see a function without an exponent in the denominator, it is a natural log answer. The reason is is that you can’t integrate term with a division sign.
In this case the x has an exponent of 1 ( x^1), you always have to move the denominator to the numerator to eliminate the division sign before you can integrate. If you move the x^1 to the numerator to eliminate the division sign it becomes x^(-1) so when you do the integration process which is always add 1 to the exponent and divide the term by that answer, However when you add 1 to a -1 you get zero, and any term to the zero exponent = 1, so that’s why the natural log comes in. In the first integral above = ln(x), then you can enter the ranges for x that you are given, do the top range first and subtract the bottom range to get the answer (area under the curve of the function). The second integral above you’d break it into two integrals ∫[1/(c+b)] dx which equals x/(c+b) and then the second term 1/[(k+x)]dx which equals ln(k+x).
3 Calculus Questions Solved by TI-89
I’m really trying to figure out how to use your program with a couple different problem examples:
“Find the following derivatives of f(x). Do not leave any negative exponents”
1. F(x)= 4^x-ln(2x^2-x)
What program can I use to solve this?
another is f(x)=2csc(x)+5arccos(x)
This is fundamental to calculus and you must start to learn it or know it.
Notice the minus sign between the terms (if a plus no difference)
This means that the derivatives of the terms are separate or individual
You differentiate each by itself and one at a time
There could be 15 more terms each separated by a minus or plus and you’d do each one separate.
So: f(x) = 4^x f’(x) = x*4^(x-1) Notice when differentiating you take the exponent
Multiply it times the front of the term and take one away from the exponent.
You must do this process in your sleep and fast or you’ll have trouble passing calculus
Another Example
f(x) = 15x^7
f ‘(x) = derivative
= 7*15*x^(7-1)
= 105x^6
Integration is the exact opposite
You add one to the exponent first
Then divide by that new exponent
∫[105*x^6] dx
= 6+1 = 7
So: 105*x^7 / 7
= 15x^6
Problem 1) the trig problem
Reload the attached program
First Delete the same named program from you calculator
Then reload the attached changing to “Archives” first
For the problem go to:
“trig” in my menu
Scroll to csc(x)
Find the derivative and add the 2 in the front of the answer
For arcos(x)
Scroll to cos-1 in the menu of trig
And find that derivative adding the 5 in front
“Answer the following questions about the given function: f(x)=x^3-6x^2+9
A) Find f'(x)
B) Find f”(x)
These again are separated by minus and plus signs so each is differentiated separately
f(x) = x^3 – 6*x^2 + 9
f ’(x) = 3x^2 – 12x + 0
f ‘’ (x) = 6x – 12
Notice I took the exponent and multiplied it by the front of the term
And then took one away from the exponent in each case.
Do these in your sleep!!!!!
Use log differentiation to find the derivative of the following function with respect to variable x.
(x^3+2)^3sqrt(2x^2+3)
Notice the “times” sign so you’d be thinking “product rule” or logs to differentiate
First it must be expanded:
I have expanded log problems to another base
But haven’t programmed to expand natural logs, but am in the process.
Should be done soon
(x^3+2)^3 * √(2*x^2+3
ln((x^3+2)^3) + ln(√(2*x^2+3) (always you change a square root to ^(1/2)
= ln( (x^3+2)^3 ) + ln( (2*x^2+3)^(1/2) )
= 3*ln( x^3+2 ) + (1/2)*ln( 2*x^2+3 )
Now you can choose in my menu
“log Problems”
Choose “ln(x)”
Choose “differentiate”
And add the above ln tems one at a time
Put the problem back together when finished with the individual solutions.
Calculus Q & A
Can the Calculus App do the Following?
F(x)=6x^-5
F(x)= 6x^4-4x^3+5x^2
Answer:
f(x) = 6x^5 would be “derivative/algebra” for differentiation
Calculus Final Solved Question 5 | Every Step Calculus
Calculus Final Solved: Question 5
Calculus Final Solved Question 2 | Every Step Calculus
Real Calculus Final Solved with TI-89 App: Question 5
Optimization | Max Area Enclosed by Rectangle | TI-89 Calculus App
Optimization for Max Area Enclosed Rectangle on TI-89: Raw Transcript
This is a video from every step calculus dot com
demonstrating how my progams work on a t i eighty nine titanium calculator
and other calculators in the t i system for physics and calculus problems
ok this is an optimization problem in calculus and ah with regard to finding the area
given a amount of fence which is a usual problem in calculus
ah and let’s get started you put second alpha
you push second alpha to put in the i n d e x letters
and then press alpha and put in the eight and open and closed parenthesis
press enter and you’re into the menu calculus one menu
and we’re going to scroll down here to go to fence area
and we’re gonna press enter on there and a certain amount of
using a certain amount of fence how much is them maximum of area etcetera
given one side of a river and were going to put in maybe
you have to press alpha before you put any a numbers or any
characters in these lines of my programs so well press alpha
and were gonna put maybe eight fifty for the maximum fence that you have to work
with I always show you what you’ve entered
so you can change it if you want I say it’s ok
here’s a picture of it here’s the river
and you got the x on each side and the length of the other side
and generally in a problem or a test their going to ask you find the equation
for the length, here’s the equation eight fifty minus two x
write that on your paper here’s the area function
x times w and here’s the function here
write this on your paper eight fifty x minus two x squared
we multiplied x times eight fifty we take the derivative of that
here’s the derivative eight fifty minus four x
write that on your paper you gonna look like a genius
and we’re finding a critical number really critical number is not a critical point
because you haven’t found the y you’ve just found the x value
notice we took the derivative and then did the algebra computation
to find the x. write this on your paper
and here’s what you’ve found you found two thirteen on this side
two thirteen on this side and four twenty five for the length
just in case you’re interested in that they don’t generally ask you that
but they might you plug the critical number into the
original function to get the maximum area actually you’re getting the critical point
then and you do these computations and notice
that the area is ninety thousand three hundred thirteen
square units if its feet that would be square feet
if it’s meters what ever and this actually the point would be
eight fifty for the x and ninety thousand three hundred thirteen
for the y and pretty neat huh
every step calculus dot com go to my site
buy my programs and pass calculus
Calculus Cheat Sheet: EveryStepCalculus.com
Use the TI-89 as the Ultimate Cheat Sheet
..
My name is Tom and I program TI-89 calculators to be the Ultimate step by step Calculus Cheat Sheet. The app show all work right on the calculator screen.
The programs are a Compilation of Midterms, Final Exams and homework from college calculus classes 1,2 and 3 all over the United States. The app shows work for calculus solutions line by line at your own pace so you can write it down on tests, homework, whatever.
You get all the calculus 1,2 & 3 programs below for the price of a serious happy hour. That all four years of calculus, updates forever included.
100% Guaranteed or your money back
LEGENDARY SUPPORT:
Phone Support (my favorite) | Email Support | Facebook Support | Twitter Support
I do it ALL and it is IMMEDIATE!
CALCULUS 1 PROGRAMS (Scroll down for 2 & 3)
Chain Rule | dy/dx = f’[g(x)] * g’(x) | dy/dx = f’(u) * u’ | (5x²+7)^5 | sin(ax) | 7*cos(5*x^2) | (tan (5x))^5 Video Example
Concavity
cos(a * x) derivative
cos(a * x) integrate
Critical Points Video Example
Definite Integral | = ∫ [ f (x) ] dx Video Example
Definition of a Derivative
Derivatives/Algebra (step by step) | √(x) | 3√(x) | 5/√(x) | 5/x | 5/8x | 5/x² | (5x)² | 5x²/8 | x(x+5) | x^½ | x^(-½) | (x²-4)/(x+2) | (x²-4)/(x-2) | (5x²+7)^5 | √(5x²+7) | (5x²+7)½ | ³√ (5x²+7) | (5x²+7)¹/³ | sin | cos | tan
Difference Quotient Video Example
ê(x) Derivatives
ê(x) Integrals
Equation of a Tangent Line (y=mx+b) Video Example
Equation of a tangent line at a pt | (y = mx + b) Video Example
Graphing by Hand | Concavity | Critical Points | Crosses x axis | Inflection Point | Intervals of Increase | Intervals of Decrease | Local Max & Min
Local Max and Min Video Example
Implicit differentiation | y³+y²-5y-x² = -4 Video Example
Integrals/ Algebra (Rewrite selected & Integrate) | n / √(x) | (x² + n)² | (x³ + n)/x² | ³√(x) | n / x² | n / ³√(x) | n / x√(x) | 1/x³
Integration by Parts | ln(x) Video Example | n*e^x Video Example | sin(x) Video Example | cos(x)
Intervals of Increase or Decrease
Limits Video Example
In(x) Natural Log
log(x) Log to Other Base | Evaluate | Solve for x | Exponential Form | Logarithmic Equation | Differentiate
Product Rule | ( f (x) )( g (x) ) Video Example
Quadratic Formula
Quotient Rule | ( f (x ) ) / ( g (x) ) Video Example
Relative Extrema
sin(a*x) Derivative
sin(a*x) Integral
Trig & Half Angle Formulas & Identities | cos(2x)2 | 1-cos(2x) / 1+cos(2x) | sin²(x) + cos²(x) = 1 | tan(x) | tan²(x) | Trig d/dx cos(2x)/2 | cos(2x) | cos(x) | cos²(x) | cot(x) | csc(x) | csc²(x) | sec(x) | sec²(x) | sin(2x) | sin(x) | sin²(x)
Trig d/dx Identities
U – Substitution
Recent Testimonials Summer 2013:
Tom- I showed my ex, who is a calculus professor, and he was waaaaaaay impressed. And he is an arrogant ass, who never helped me ever…I could tell he wanted to hate on it, but he couldnt.
Kristin P
Tom…I think that I’m finally done with Calculus II. In the prior test I got 78 and yesterday I finished all the problem on the test. I think I should be able to remain around the same grade. Thank you so much for your help; your programs really made the difference. They didn’t just solve the problems for you, in my case, they gave me the confidence and security I had lost with those stupid professors and the way they teach. To be honest, studying the programs on my calculator taught me how to solve problems that I couldn’t do before due to the way they were presented. I felt confident and secure yesterday, and it only possible because either I remember how to do the problems or the calculator would. Thanks one more time for time, dedication and quick responses. There is no other person in the whole world that would do what you do for us , college students being killed with freaking calculus classes. John
Tom- Got it to work with that link you sent me! Just wanted to say thanks for all the great work you do, and for helping me pass this calculus class. I’m going to tell everyone about this and make them pay the $30 dollars because you have done a splendid job programming my friend. Let me know if you have any new programs for derivatives or integrals and Ill let you know if I need any more help! Much thanks, –Eric
I basically just needed to say that you’re an amazing man. Basically saved my life during my emag theory course
-DoubtingThomas (Youtube vectors review here)
oh my god I figured it out. You’re the freaking best! -Sarah
Thanks Tom. I appreciate you taking the time to break down and explain these to me. :0) –Nelson
Tommy, Great talking with you last night. I already liked you for developing this “most excellent program” but after our conversation I concluded you to be a great guy. I’ve been playing with this program most of the night, took in a few “z’s” and am back for more. This program really is superb. I did, however, notice that for some unknown reason when I attempt to do Relative Extrema’s and Trajectories that both programs came up as “Program not Found”. I’m not sure if I will be encountering the Trajectory stuff in this semester of Calculus but I do have a test this Thursday that includes Relative Extrema. Any suggestion, oh Master of this great creation?! I’m going to be gone most the day but should be home late afternoon if you got time to call. Same number (843-xxx-xxxx). That’s Myrtle Beach, 3 hours ahead of you and more golf courses than you can shake a stick at. Thanks -Joe
Wow! Awesome! These are great, so great, thank you! -Kristen
Tom is the man! His program is helping me pass my calculus class. He was willing to help me immediately when I couldn’t get one of the programs working! This application is in my opinion a STEAL! I’ve never met Tom in person but I’ll owe passing this class to every step calculus.
-YouTube product rule video comment
CALCULUS 2 & 3 PROGRAMS
A & B Vectors A(x,y,z) B(x,y,z) ||A|| Magnitude ||B|| Magnitude | A – B | A – B Magnitude | A + B | A + B Magnitude | A + B + C | Find Resultant | Find Components | A * B Dot Product | | A x B Cross Prod | B – A | n * A | (n * A) + (n * B) | Area of a parallelogram | Component A direct B | cosine(AB) | Equation of a Plane | ax+by+cz+d=0 | P&Q Points | Projection of A on B | Projection of B on A | Unit vector A | Unit vector B Video Example
Acceleration | r(t) function
Angle of a Vector | r(t) function
Arc Length | f(x) system | r(t) system | y system
Average Rate of Change
Component of A Direction of B
Conservative Curl
Compute Curl at a Point
Compute Divergence at a Point
Cosine(∅) of A & B
Curl | Definition | PQR notation | Conservative | Divergence | Curl Problem | Compute Curl at Point | Compute Divergence at Point | MNP notation | Conservative | Divergence | Curl Problem | Compute Curl at Point | Compute Divergence at Point Video Example
Cross Product Video Example
Definite Integral Video Example
Divergence of Curl
Divergence of Vector Field
Dot Product Video Example
Eliminate the Parameter (t)
Gradient | Definition | 2 Variables | 3 Variables
Implicit Differentiation Video Example
Trig & Half Angle Formulas | 1 + cos(2x)2 | 1 – cos(2x)/1 + cos(2x) | 1 – cos(2x)/2 | cos(2x) | cos(x) | cos²(x) | cot(x) | csc(x) | csc²(x) | sec(x) | sec²(x) | sin(2x) | sin(x) | sin²(x) | sin²(x) + cos²(x) = 1 | tan(x) | tan²(x)
Linear Equations (3 variable) | ax+by+cz+d=0
Line Integral Over Range | = ∫ ( f [(x(t),y(t),z(t)] * √ [ x'(t)² + y'(t)² + z'(t)² ] ) dt
Mass of Spring or Wire
Magnitude of a Vector | r(t) function
Parametric Equation | r(t) function
Partial Fractions Integration
Polar to Rectangular Conversions
Projection of Vector A on Vector B
P & Q Vector Points | Position Vectors | Projection of a on b, b on a | Speed
Quadratic Formula
Sketch a Graph | r(t) function | Make a Table of Points
Surface Integral | x,y | x,z | y,z
Position Vectors | Velocity | Acceleration | Speed | Unit Tangent Vector | Parametric Equation | Standard (Linear) Equation
Speed | r(t) function
Sphere | Center Point | Mid Point | Equation | Radius
Surface Area Revolving
Surface Integral | x,y | x,z | y,z
Tangent Plane to a Surface
Trig d/dx – Identities and Functions | Half Angle Formulas | Reciprocals | Integration | Derivatives | 1+cos(2x)2 | 1-cos(2x) / 1+cos(2x) | 1-cos(2x)/2 | cos(2x) | cos(x) | cos²(x) | cot(x) | csc(x) | csc²(x) | sec(x) | sec²(x) | sin(2x) | sin(x) | sin²(x) | sin²(x) + cos²(x) = 1 | tan(x) | tan²(x) Video Example
U Substitution
Vectors | Unit Tangent Vector | Unit Vector PQ/||PQ|| | Vector Between P & Q
Velocity
Volume of a Parallelepiped
Work | Force Field | Lifting Object | Spring | Pumping Oil
Don’t forget the programs come with my
LEGENDARY SUPPORT:
Phone Support (my favorite) | Email Support | Facebook Support | Twitter Support
I do it all and it is immediate.
………..[ahm-pricing-table id=1330 template=gray]
Calculus Cheat Sheet Video Transcript
What Professors don't tell you about ln(x)
Any problem with ln(x) in it you’d choose ln(x) in my program menu
When differentiating ln(x) and when using the product rule which is necessary, where the function might be something like 5*ln(6x). You have two functions –—— 5 and ln(6*x). Two functions mean f(x) and g(x).
In my programs I used in this case 5 for f(x) and ln(6*x) for g(x)
And you have the formula for product rule, h ‘ (x) = f ‘(x) * g(x) + f(x) * g ‘ (x)
Don’t worry – I do all of this for you – step by step – in my programs, however I want to mention here of again what professors don’t tell you or make you aware of, and that is
If ln(x) has a + sign or – sign in it, it makes a difference which one you use for f(x) or g(x) so for instance in a function like 5*ln(6x+1), you have to use instead of 5 for f(x) (like above) — ln(6x+1) for f(x)
Now who told you or me about that little detail in our calculus life?
Incidentally any derivative for ln(x) has a special formula which is:
u ‘ / u
u is what’s inside of the parenthesis.
Have fun with my programs and pass calculus, never to use it again !!!
Tom

