TI-89 Calculus |Radius of a Sphere

June 9, 2015 by Tommy Leave a Comment

Find the radius of a sphere. Give two points on its circumference.

Points are P=(7, -2, -6) and Q= (5, -9, 4)

Raw Transcript

Hello everyone, Tom from everystepcalculus.com, everystepphysics.com. We’re gonna do a calculus three problem regarding a sphere. And we’re given two points on it’s circumference. Outer shell, you know. And let’s do it. Index 8 to get to my menu,

find the radius. Scroll up to get to the bottom of the alphabet, cause the sphere radius is in the S’s and closer to the W’s than the A’s. There’s sphere radius there. Choose that one. We’re gonna put our points in.You have to press alpha first. Alpha 7, Alpha minus 2. Alpha minus 6. Alpha 5 Alpha minus 9. Alpha 4. I always show you what you’ve entered, you can change it if you want. Looks okay. Now I’m gonna find the radius number 4. Here’s the formula. Write this stuff on your paper. And R equals these calculations here, just as if you did it yourself without mistakes. And the answer. Pretty neat, huh? Everystepcalculus.com, go to my site, buy my programs if you want to pass calculus, and subscribe if you want to see more videos from me. Have a good one.

Find the Standard Equation of a Sphere

June 9, 2015 by Tommy Leave a Comment

Find the standard equation of the sphere.

Let P1 = (-7, -9, 7) and P2 = (0, 1, 1) be endpoints of a diameter

Raw Transcript

Hello everyone, Tom from everystepcalculus.com, everystepphysics.com. A problem regarding a sphere and the standard equation a person submitted, and let me show you how I do it in my programs. Index 8 to get to my menu, my main menu. I’m gonna scroll up to get to the S’s at the bottom, it goes to the bottom of the alphabet so it’s easier and quicker to get there. You can press second and these cursors to go screen by screen on your calculator. Those are all the choices you have, and we’re gonna have sphere equation.

And we’re gonna enter our P, Q points. All professors do things different, which I’m against in calculus. Well, I’m not too thrilled about calculus at all. We have p1 and p2 here, in most cases it’s P and Q points. You have to press alpha before you enter anything in these entry lines here. Alpha, the first one is minus 7. There it is. Alpha minus 9. 7 is the P point. These are point on the outside of a sphere, and they give you two points are you’re supposed to find the radius. And different types of things. Not easy. Even if you know the formula it is not easy, you’re gonna mess up on the minus signs or whatever. That’s why the program steps up so you don’t mess up, and I didn’t mess up. The Q point is Alpha 0, Alpha 1. Alpha 1 for the Z point. I always show you what you’ve entered you can change it if you want. I say it looks pretty good. And we’re gonna choose equation, standard equation, number 5. There’s the formula. And you have to find the xo, yo, zo first Which is this system here. That equals this. Standard equation that is these entered into the equation. Here’s the standard equation. Pretty neat, huh? Everystepcalculus.com. Now I noticed, with the minus in minus, you might have to think in life a little bit, so you might have to say, oh there’s a minus and minus, minus times a minus is a plus. So you might put on your paper, x plus 7, over 2. Or same thing with y. Y equals minus, minus a minus, which is equal to a plus. Which would be y plus 4, and this would be z plus 4. So, keep that in mind. Have a good one. Everystepcalculus.com, go to my site, buy my program if you want to pass calculus. Subscribe if you want to see more movies from me. Thanks and have a good one.

Vector Function on TI-89 & Titanium

June 7, 2015 by Tommy Leave a Comment

Raw Transcript

Hello everyone, Tom from everystepcalculus.com everystepphysics.com, a quick example of

vector valued function, r(t) formula, or vector function. And with regard to speed. So, let’s do it. Index 8 to get to my menu. We’re gonna scroll up to get to the bottom of the menu so that we’re closer to the s section; it’s all alphabetical. I choose speed. Speed is a scaler, meaning it has no direction, it has magnitude, but no direction. Unless time is added to it, and then it does have a direction. You’re gonna enter these values here, but if Z is not given you’re gonna enter 0, okay? So, you have to press alpha before you enter anything in these entry lines here. Alpha minus 3 times T Alpha 2 times T Alpha minus 6 times T. I always show you what you’ve entered, you can change it if you want. There’s the vector. These indicate that it’s a vector, these arrows here. Say it’s okay. Now we’re gonna choose speed, we’re looking for speed. It’s right there. And it’s given by the magnitude. Magnitude is the derivative of the function times the squares of each one of them. So it’s X prime of t squared, y prime of t squared, z prime of t squared. And the derivatives are minus 3, 2, and minus 6. And we square them. Asks if there’s time given, I’d say there’s no time given in this one. So we’re gonna choose number 2. And then just square the values, sum them up,

49, and there’s the answer: 7 units per second. Pretty neat, huh? everystepcalculus.com, go to my site, buy my programs, and subscribe if you want to see other videos. Have a good one.

Find Midpoint of Sphere on TI-89

June 7, 2015 by Tommy Leave a Comment

Find the midpoint of a sphere.

Let P = )5, -2, 3) and Q = (0, 4, -3) the endpoints on the circumference sphere.

Raw Transcript

Hello again everybody this is Tom from everystepcalculus.com, everystepphysics.com.

We’re gonna do some calculations in a sphere. This is generally calculus three. And we’re gonna find the midpoint, or center, of a sphere. Index 8 to get to my menu. You can scroll up to get to the bottom of the menu so you can get to the S section quicker. You can press second and the cursor here to get screen by screen instead of one click like I’m doing. This is a simulator. Now we’re gonna choose here, center and midpoint. We’re gonna enter our P and Q points pressing Alpha first. Alpha 5. minus 2 Alpha 3 The Q point is Alpha 0, Alpha 4

Alpha minus 3. Now we gotta go back and change them. Alpha 5 Alpha minus 2 Alpha 3 Alpha 0 Alpha 4. And Alpha minus 3. I always show you what you’ve entered, you can change it if you want, which we just did. Say it’s okay. Now I’m gonna press number 1. Number 3 for midpoint Here’s the calculations: xo, yo, zo. And the answer. Everystepcalculus.com, go to my site buy my programs if you want to pass calculus.

And also subscribe so you can see other videos I might make. Hey have a good one.

Shell Method

June 2, 2015 by Tommy Leave a Comment

Raw Transcripts
Hello, everystepcalculus.com. A problem regarding Shell Method and the axis of rotation is vertical. A Yahoo problem. Let’s do it. Index 8to get to my menu. You need to get to the s’s of the alphabet so you have to go down to the bottom of the alphabet by going up and then clicking up to go to finding shell. And it is there. And we have the choice of horizontal axis or vertical axis, we want this problem is vertical axis. There’s the formula. And it’s taken me a long time to program this stuff, but if (p)x is the radius, if it’s not given enter x for p(x), okay, cause there’s two functions, p(x) and h(x). And sometimes it’s more elaborate than this one is. You have to press alpha before you enter anything into these entry lines so I’m gonna…. here’s p(x) here, alpha x I’m gonna enter. And for h(x) is the problem, alpha 6 minus x. 1Oops. 6 minus X. I always show you what you’ve entered you can change it if you want, that’s okay, now, I press number one. One of the tough things about shell is the confusion of the whole thing, and the nonsense of the whole thing, but then we’re gonna find the A&B limits. You do that by– if nothing else is given for the x value, than the x is equal to 0 because you got a vertical axis of revolution. It’s vertical, and we set the X at equals zero point. So we set the equation equal to that. 0 equals 6 minus x, we get the limits, it’s six. This is where the function crosses the x-axis. So, here’s the equation now for the integral. And so we have this issue. Mark this on your paper.
When we do the integration, here’s the integration of the function. And, as we substitute at x equals 6, the limits, it’s 72 pi and x=0,. we get 0. Upper limit minus lower is 72 pi.Have a good one.

Integral Calculator With Steps

June 2, 2015 by Tommy Leave a Comment

Raw Transcripts
Hello, everyone. This is Tom from everystepcalculus.com. There’s been many, there’s always requests for Integral Calculator with Steps and that’s exactly what my programs do. And Integration is one of the toughest things in Calculus. It was for me when I was in class. I hated Calculus. You probably feel the same way and I’ve found nobody that likes Calculus. Except maybe Professors. But anyways, I’m going to show you how my programs work on U Substitution. Index 8 to get to my menu. I’m already at U Substitution. I have scrolled there. We’re going to enter our function. You have to press Alpha before you enter anything into these entry lines, here. Alpha 6 times x to the fourth power times the quantity parentheses 3 times x to the fifth power plus 2, close off the parentheses to the sixth power. I always show you what you’ve entered. 6x 4 times 3 x quantative to the 5 plus 2 to 6. Looks
good to me. I say it’s okay. And we’re going to work the problem. Busy means the program is loading. We’re going to evaluate this. First we rewrite it where all constants come out of the integral. And then we put the x to the 4. The way that you know that any problem is U Substitution is that you look immediately at what’s inside the parentheses. You take the derivative, right now you should be able to do, this is 15x to the 4. Right now in one second, you should be able to know the derivative of that. And you notice that x4 is on the outside, too. If it isn’t, it’s not a U Substitution problem. It has to be converted, okay. So I do all that for you, really. But that you have some understanding of how you do U Substitution. U is equal to this, du is equal to this and then we make this the other trick, this whole system here took me about a year to figure this out in a system that works, you know. And so, this always has to be x to the 4 dx over here so you have to take the 15 and divide the du by that on the other side using Algebra, of course. And so it works the problem. 6, you take of course the du with the 6 here, you have a du with a 15 notice the 15 come out of the, here’s the constant again so that comes out of the integral and goes in front right here, see it right here. 6 times that, of course, with the 2 fifths. etc, etc. Here’s the answer to your problem right here. Have a good one. everystepcalculus.com

ln(x) Integration

March 25, 2015 by Tommy Leave a Comment

Raw Transcripts

Hello, everyone. This is Tom from everystepcalculus.com, everystepphysics.com. I’m going to do a integral of a natural log in this video to go with my menu. Let’s do an index 8 to get to my menu. I’m already at LN of X integral, which is natural log of you know, and integrate that. We’re going to press number 2, integration. And we’re going to integrate transcendentals. Number 1, log of X. And you have to press alpha before you enter anything in these entry lines here. And we’re going to enter the function that you see. Alpha 2nd log of 5 times X. It will show you what you’ve entered; you can change it if you want. I say it’s okay. I’m going to rewrite this. Like you see, integral of log of 5x and then we have the 1 over here, DX, to show you that we’re going to do DV is equal to 1, V is equal to the interval of 1dx. The answer is X. And then U is log of 5x, but that always equals the derivative of that is one over X. Here’s the formula: VU minus the integral of VDU. And we plug in the variables for the formula. Here’s V and here’s U, minus the integral of V again and then DU. And then we’re going to integrate 1 here, because that’s what that works out to, what we just put down before. And so the integration of integral of 1 is minus X. So here’s the answer: X times log of 5 times X minus 1 plus C. Notice we’ve factored the X out here. Also notice that sometimes‚ you might think about this too‚ log of 5 times X is really log of 5 plus log of X, so that could be written like that, too. X times log of 5 times log of X minus 1 plus C. So subscribe at my site and you can see more movies that I might make for your enjoyment. Have a good one.

Line Integral

March 25, 2015 by Tommy Leave a Comment

Raw Transcript

Hello again; Tom from everystepcalculus.com, everystepphysics.com. I’m going to do a line integral in calculus 3 physics. This is right off of Paul’s notes, his example. You can check if you Google line integral. None of us are interested in line integrals; all we want to do is know how to do the problem to pass a quiz or a midterm. Very difficult. I’ve tried to find what does a line integral represent. In other words, what’s the SI units for the answer that they get, and I can’t find it. So that shows you something about calculus. To me, most of it is nonsense. Index 8 to get to my menu. I’m going to scroll down to line integral. I’m already there to save time. And we’re not in a vector field we’re given the RT situation. And I show you the formula; this here is the formula: RT times the magnitude of R of the derivative of RT. And then this worked out. This is RT here, and then the magnitude absolute value of R, derivative of RT is this. Write this all down in your paper, exactly as you see it so you look like you know what you’re doing. And we’re going to put the RT was given in this a problem. We’re going to do alpha before you enter anything into these entry lines here, alpha 4 times 2nd cosign of T alpha 4 times 2nd sign of T. And when they don’t give you the Z, you just put 0 in. Alpha 0. Now it will show you what you’ve entered; you can change it if you want. I say it’s okay. Now we start working out the‚this is a vector here when you have these arrows on these sides, it’s called a vector, RT vector. We’re doing the derivative of that, which equals minus 4 sign of T and 4 cosign of T, et cetera. And we do the magnitude, which is squaring those derivatives. And the answer turns out to be the square root of 16, which is 4, really. And then we’re going to enter the function given, which is alpha X times Y to the fourth power. Where they dream up all these nonsense formulas and functions is unbelievable in calculus. I say it’s okay; you could have changed that if you want. So for the range of alpha, minus pi divided by 2 to the range of alpha pi positive divided by 2. So here we have the range, and here we have the function, and here we have the derivative magnitude of the derivative of RT function. And you do the calculation just as you see them here on your paper. Over the range of this here, you’ve already done the derivative here. Here’s the derivative of that. The answer is 8192 over 5. Notice now it’s just an arbitrary number. We’d like to know area or something, distance, or length or something, but it’s just a number. So you have to decide yourself how important that is. I mean, to me, how important is the slope of a line, which is the derivative or the area under curves, or volume under functions, under spheres and stuff. Have a good one. Go to my site, subscribe and you can see more movies that I might make.

Antiderivative Calculator

March 22, 2015 by Tommy Leave a Comment

Find the Antiderivative of: √(6x-1)

Raw Transcript

Hello again everyone, this is Tom from everystepcalculus.com, everystepphysics.com, I’m gonna show you how to turn your titanium calculator with my programs into a antiderivative calculator. Okay, so, index 8 to get to my menu. I’m gonna do a U substitution, because most problems are U substitution integration and antiderivative is really doing the integral of a derivative. Where as an integral itself is doing an integral of a function which might be a derivative or not. But antiderivative is really an integral, and it’s an indefinite integral because you have to have a plus C at the end and somebody has to decide on the C, there’s 10 million integrals for an indefinite integral, all decided by what the plus C is. Who decides that, I have no idea. U substitution, enter a function, you have to press alpha before you enter anything into these entry lines here, don’t forget that. Alpha and the square root second square root. And the square root of 6 times X minus 1. Close off the parenthesis. Oh, didn’t press alpha I guess. 6 times x minus 1. That’s better. Now we show you what you’ve entered, you can change it if you want. Say it’s okay. And we’re into the problem. U is whatever’s in the parenthesis, you should be able to do the derivative of whatever’s in here in a second okay, in your sleep– for instance, the derivative of 6x is 6. Well here you have U of 6x minus 1, and the derivative is 6dx. We want to always have the dx by itself, because the dx is by itself up here, right. So you’re gonna take this and use algebra, and bring it over to the other side, and divide du by 6. That equals (1)dx over here. So now, the square root of u then is equal to the square root of 6x minus 1 because we made this u. So that equals the integral of u to the one half, because if this was a cube root it would be one third, if this was the fifth root it’d be one fifth here. But this is the square root, so it’s the one half. And then you have to add the du divided by 6, which we formulated before. That’s one of the big tricks in u substitution that took me 10 years to figure it out. So we have to bring all constants out of the integral, which we do here, one sixth here, we add 1 to the 1/2 here, which becomes 3, 3 halves, divided by 3 halves, so you have one sixth when you divide by a fraction, you invert multiply, so we inverted the fraction. Two thirds. And the answer’s 1/9th, 6 to that. Pretty neat, huh? Everystepcalculus.com, go to my site, buy my program if you want to pass calculus and do your homework. Have a good one!

Difference Quotient Solver

March 20, 2015 by Tommy Leave a Comment

Difference Quotient Solver

Step by Step Calculus Solver

March 18, 2015 by Tommy Leave a Comment

Step by Step Calculus Solver

Raw Transcripts

Hello, Tom from everystepcalculus.com, everystepphysics.com. Don’t forget physics, either, in your schooling. I‚m going to do two problems in calculus: a definite integral, and a log problem. I’ll show you the diversity of my programs. And my programs turn the titanium into a calculus calculator with steps. A calculus calculator with steps‚ that’s exactly what my programs do. So let’s do it. Index 8 to get to my main menu. We’re going to scroll down to definite integral in the D’s. Definite integral in X because you only see X in the problem, right? We’re going to enter the function. You have to press alpha before you enter anything into these entry lines. You’re going to press alpha, and we‚re going to enter the function. 3 minus X to the cubed plus 4 times X. Now we show you what you’ve entered; you can change it if you want. I say it’s okay. I’m going to enter the range. Lower range is alpha minus 2. Upper range is alpha 2. I say that’s okay also. And we integrate it, which is this right here. We’ve integrated each one of those terms, separated by plus or minus signs. And at the upper range, X equals 2. You add these into the‚ you’re going to use, instead of quotation marks, you’re going to use parentheses around your additions into the main function. But it equals 10. And if X equals minus 2, the answer is minus 2. Upper minus lower is equal to 12 square units. Pretty neat, huh? All right, we’re going to go back to the main menu. Number two: And we’re going to scroll down. Now this is in the L section, logs. So I’m going to do this quick. Behind the simulator here I can only use, I only have one essential finger to do this with. On your calculator, the titanium, you can hold the 2nd down with your thumb or finger and press this. It’ll go screen by screen and really go quick down to logs. We have natural logs and all kinds diversity in my menus. I’ve done all the calculus problems, or most of the tests, of course. Nobody can do all of the calculus problems; there’s millions of derivations of that. Log problems, okay. We’re going to evaluate this log problem, number 3. We have to press 2nd alpha to get to the letter register to put log in. We’re going to enter the problem. We want to make, we have 2nd down here, but we want to turn it to black like that. Then we can put the logs in there, so that’s‚Äî The letters appear over the numbers, you can see them. And then we’re going to go back to numbers, which erases that black mark there, indication. And we’re going to put 3 parentheses 1 divided by 27. Close off the parenthesis. And I show you what you’ve entered. It looks pretty good to me. We’re going to press 1, and here’s the answer step-by-step. In other words, if you on your calculator, if you put 3 to the exponent minus 3, you’re going to come up with 127. All right. Pretty neat, huh? Everystepcalculus.com. Go to my site. Buy my program if you want to pass calculus or physics. Or subscribe so you can see more videos. Have a good one.

Implicit Differentiation Calculator With Steps

March 17, 2015 by Tommy Leave a Comment

Implicit Differentiation Calculator With Steps

Raw Transcript

Hello everyone; Tom from everystepcalculus.com and everystepphysics.com. Don’t forget physics. I have turned through the use of my programs, or for programming, your titanium calculator into an implicit differentiation calculator with steps. And that’s exactly what my programs do. So let’s do it. Index8() to get to my menu. I’m already at implicit differentiation. I’ve scrolled there. On your titanium, if you want to go to my menu and go down quickly, you hold the 2nd button down here and then use the down cursor here. We’re already at that, so. And then enter the function. You have to press alpha before you enter anything in these entry lines here. And the problem is alpha Y squared plus 3 times X minus 8 times Y plus 3 equals 0. Now it will show you what you’ve entered, and you change it if you want. I say it’s okay. You’re differentiating all of the terms on both sides of the equals sign. You must have a 0 or a constant on the right of the equals sign. You have to use the algebra to make that happen if they give you a more difficult problem, or a different look at a problem. And so we differentiate each one of the terms. I do that for you; you write this on your paper as we go through it, exactly as you see it here. And we combine the DY DX terms, separate it from the other terms, and here’s the answer right here. Now we want to evaluate it at a point, so we’re going to press the X value is alpha 4 and alpha 3. I show you that also; it looks good to me. So we’re substituting 4 and 3 for the X and the Y values and then find the derivative. Cut them to one half and the slope of the line is 333 degrees. That means that the slope is going to be here’s 360 going this way. Here’s 270 going down. So the slope is going to be like this. Pretty neat, huh? Everystepcalculus.com. Go to my site. Buy my programs if you want help passing calculus. Or subscribe to enjoy more videos that I might make. Have a good one.

Learn more about implicit differentiation on your calculator

Implicit Differentiation test question solved by TI-89

Implicit Differentiation calculator – Video Example #2

Implicit Differentiation at a Point – Video Example #3

Implicit Differentiation – Video Example #4

Calculus Calculator with Steps

March 16, 2015 by Tommy Leave a Comment

Calculus Calculator with Steps

Raw Transcripts
Hello, Tom from everystepcalculus.com, everystepphysics.com. Don’t forget physics, either, in your schooling. I’m going to do two problems in calculus: a definite integral, and a log problem. I’ll show you the diversity of my programs. And my programs turn the titanium into a calculus calculator with steps. A calculus calculator with steps, that’s exactly what my programs do. So let’s do it. Index 8 to get to my main menu. We’re going to scroll down to definite integral in the D’s. Definite integral in X because you only see X in the problem, right? We’re going to enter the function. You have to press alpha before you enter anything into these entry lines. You’re going to press alpha, and we’re going to enter the function. 3 minus X to the cubed plus 4 times X. Now we show you what you’ve entered; you can change it if you want. I say it’s okay. I’m going to enter the range. Lower range is alpha minus 2. Upper range is alpha 2.
I say that’s okay also. And we integrate it, which is this right here. We’ve integrated each one of those terms, separated by plus or minus signs. And at the upper range, X equals 2. You add these into the you’re going to use, instead of quotation marks, you’re going to use parentheses around your additions into the main function. But it equals 10. And if X equals minus 2, the answer is minus 2. Upper minus lower is equal to 12 square
units. Pretty neat, huh? All right, we’re going to go back to the main menu. Number two: And we’re going to scroll down. Now this is in the L section, logs. So I’m going to do this quick. Behind the simulator here I can only use, I only have one essential finger to do this with. On your calculator, the titanium, you can hold the 2nd down with your thumb or finger and press this. It’ll go screen by screen and really go quick down
to logs. We have natural logs and all kinds diversity in my menus. I’ve done all the calculus problems, or most of the tests, of course. Nobody can do all of the calculus problems; there’s millions of derivations of that. Log problems, okay. We’re going to evaluate this log problem, number 3. We have to press 2nd alpha to get to the letter register to put log in. We’re going to enter the problem. We want to make, we have 2nd down here, but
we want to turn it to black like that. Then we can put the logs in there, so that’s—The letters appear over the numbers, you can see them. And then we’re going to go back to numbers, which erases that black mark there, indication. And we’re going to put 3 parentheses 1 divided by 27. Close off the parenthesis. And I show you what you’ve entered. It looks pretty good to me. We’re going to press 1, and here’s the answer step-by-step. In other words, if you on your calculator, if you put 3 to the exponent minus 3, you’re going to come up with 127. All right. Pretty neat, huh? Everystepcalculus.com. Go to my site. Buy my program if you want to pass calculus or physics. Or subscribe so you can see more videos. Have a good one.

Green’s Theorem

March 11, 2015 by Tommy Leave a Comment

Raw Transcript

Hello again, Tom from everystepcalculus.com, everystepphysics.com, a calculus video on Green’s Theorem. Let’s do it. Index 8 to get to my menu. We’re gonna scroll down to the “G”‘s and choose Green’s theorem. Normally here’s the way problems are given, you know, something before the dy and something before the dy, and so I’m gonna ask you to enter those into this– in any problem, but you can see an example of what problem we’re gonna be doing right now. This is from Patrick JMT’s site, exactly the way he does it. Of course I have the program so that you can add other variables et cetera, so that’s what’s neat about programming and using the Titanium. So we’re going to enter alpha before we enter anything into these entry lines here, alpha X for the dx, and then alpha minus X squared times y squared. Green’s theorem turns a line integral into a double integral and I have found that line integrals are very difficult, I’d say it’s a waste of time, but to me as most calculus is. In fact, even, I was searching and searching line integrals and there’s not even SI units for the answer. You get some some sort of answer like 8192 over 5 or something. And there’s not even– so I don’t know what that computes and nobody else does. It’s called a line integral and it’s not a length, it’s not a width, it’s not an area… so I question that. But of course the Green’s Theorem makes it even a little bit more easy or difficult, depending on what you can do with integrals. But anyways, here’s my program on it. I say it’s okay once we enter that and of course they always give you a triangle. They give you a square, a curve, a unit circle, or two circles, or one circle. Calculus always makes something difficult out of something simple. If that’s simple. So anyways, this is a triangle, which we’re gonna choose. The object within the region is a right triangle. It has to be a right triangle because of the pythagorean theorem, which is x squared and y squared in there, which calculus can work with exponents like Newton designed it. And the first vertices given is (0,0), we’re gonna choose that. The next one is (0,y) and we have to enter something for the y, because even though these are all ones, you can’t enter something different. You can enter 5– and I have to make sure I understand that when I program. But this is alpha 1 and then that changes the one here and the last third vertices can’t be anything different than one. And we’re gonna enter the x-value for that. And that’s 1, 2, alpha 1. And so I show you what the vertices given are, if that’s correct then choose “okay”. And then something that other programs don’t give you, I draw it, because you’re supposed to draw it on your paper– adding the vertices and stuff like that, so here’s the way it’s drawn. And y equals x. Why does this equal x? Because this slope, if you graph it, is x. Okay, now what if this was 5 and 7? Well then, slope is rise over run so this would be 5– or, if the x was 5 and the y was 7, rise over run is 7/5. So it would be 7/5 x here. Right now its (1,1) x here. But you don’t see it because 1 divided by 1 is 1. So i exclude that part, but those are the kind of things that upset me– and this is the tough part to me, this was always the tough part– getting the vertices and how to put it in the integral. So here’s the formula for the Green’s theorem integral, here’s the region, and I show you this is ax over bx, you know, these are the limits. And so we add those automatically. 0 over 1 for the x, and x over 1 for the y. We’re gonna do the order of integration is gonna be dy first and then dx. So here’s the– we’re integrating this and we’re just gonna go through it quick and keep this video kind of short. At y equals 1 here’s the answer. At y equals x here’s the answer when you substitute that. I show you the substitutions in here. Here’s one substitute of that. Now, you’ll use parenthesis for this instead, I use quotes because that’s the way that the calculator operates, but you’re going to use parentheses. Two times parenthesis “one” parenthesis cubed. Times– and that’s substituting 1 for the y. And here we’re substituting x for the y so there would be parenthesis around this x here. And of course the upper limit minus the lower limit, look at the minus signs here and how it works out. I always screwed that up when I was in calculus. That’s the reason I programmed, so I wouldn’t screw up. And now we’re gonna do this integral here from 0 to 1. And… at x equals one it equals minus one fifth and zero. Subtract the upper limit from the lower. Or, lower from the upper limit. And the answer is -1/5. Pretty neat, huh? everystepcalculus.com, go to my site, subscribe and see other videos that I make. Have a good one.

TI 89 Partial Fractions

March 7, 2015 by Tommy 1 Comment

Partial Fractions solved on the TI-89 calculator.

Full Video Transcript

Hello Tom from EveryStepCalculus.com EveryStepPhysics.com there’s been many searches for ti-89 partial fractions and I’m going to show you how that works on your titanium.

You can download these programs into your titanium and do this exactly like I do it here a miracle of programming from the inventors MIT the geniuses over there. So I’m going to show you index8() to get to my menu. I’m already at partial fractions which you would scroll to when you know the title of what you’re looking for in calculus.

And we’re gonna enter the integral and that is quite long but I’m going to do it yet to press alpha before you enter anything in these entry lines here. Alpha left parenthesis 2 times X cubed minus 4 times x squared minus 15 times X plus 5 close off the parentheses.

Divide sign more parentheses x squared minus 2 times X minus 8. Remember calculus is the sudoko math in my opinion a lot of nonsense and this is, this is certainly true of partial fractions. Now you try this without a program, you can do it if you want, not me. Press ENTER, when it’s busy you’re loading the program I always show you what you’ve entered so you can change it if you want to X cubed minus 4x squared minus 15 X plus 5.

That’s crew x squared minus 2x minus 8 that’s good, let’s say ok, and so let’s do it. First thing you do is factor the denominator here, it’s loading programs again but once it’s loaded it’s quick on your calculator but these are long programs. Because the numerator is higher than or equal to then than the denominator you have to use short division.

So 2x cubed divided by x squared is 2x and that’ll be added to the answer at the end. This is a quotient that’ll be added to the answer at the end, calculator is computing and you write all this on your paper of course. A X minus 4 B X plus 2 times the factored denominator and you get this. Write this stuff down, I’m not going to explain it to you, and x equals -2 it equals this here x equals 4. We’re solving for all the a B’s and C’s equals 1/2 and x equals 4 I do that for you amazing program.

I think a equals 3 2 3 and 3 halves here’s the answer, 3 halves over X minus 4 plus minus 1/2 over X plus 2 plus. Here’s the quotient we found with short division plus C and then we even do the integrals for you remember most of these are logs because when you have something on a denominator without an exponent it has to be a log problem. It has to be a log differentiation.

So good luck in your calculus class and subscribe to me, maybe see more videos or you can actually buy the programs and enjoy passing calculus. Have a good one.

Derivative Calculator With Steps

March 7, 2015 by Tommy Leave a Comment

Find the derivative of the function using the quotient rule

y= (3-(1/x)) / (x+5)

Raw Transcript

Hello, everystepcalculus.com, this is Tom, and I’ve got everystepphysics.com also. There’s been many searches on the internet for a derivative calculator with steps and that’s exactly what my programs do. That’s what I needed for calculus and that’s what I have programmed for twenty years. Okay, this one is going to be another simple derivatives you gotta know immediately, okay. For instance, if I was to say, what’s the derivative of x to the tenth power, you should right away say 10x to the ninth power. You should automatically know this stuff. Know this in your sleep, okay, because you need to know the basics of calculus or you’ll never pass that class. Even with my programs. You’ll pass it much easier with my programs, but if you don’t know the basics, good luck. So I haven’t programmed really simple derivatives like that. But now we’re getting into quotient rule, and product rule, and implicit differentiation, and things like that so you need a program to do those that’s for sure. And quotient rule is difficult in itself. You have to memorize the formula, you have to be able to put these functions in the formula, and do it all right and somehow get that right on your test. And that’s what we’re interested in is passing tests. We aren’t interested in learning about calculus, we have no interest in calculus but we want to pass our tests. And maybe do some homework, okay. So here’s how my programs work on a derivative regarding quotient rule. We go to my main menu, Index 8, and then I’m gonna go up on the– to get to the “Q” section because “Q” is closer to “W” than the “A”‘s. I’m gonna scroll up here to quotient rule. Choose that, here’s the formula, you write this stuff on your paper so you look like a genius, okay? And we have to enter the function. Well we’re gonna have to press “alpha” in my programs. In every one of my programs you have to press “alpha” first before you enter anything into these entry lines here. Notice the format, you have to add these parenthesis, and then the divide sign, and then the parenthesis, okay. So I’m gonna do that now. I’m gonna add open and closed parenthesis, divided by, open and closed parentheses. Now don’t forget that system, okay. I’m gonna use the slider on the cursor to go back inside the parentheses of the first one. I’m gonna add my function– 3 minus, now we got to open and close parenthesis again, so I add them. Open and closed parentheses, and then use the slider to go back within the parenthesis. And then we got 1 divided by X. Now we’re gonna go inside the denominator parentheses and put in x plus 5. I don’t see the plus sign, I’m gonna go back. Make sure that there’s a plus sign… 5 … very good. I always show you what you’ve entered, you can change it if you want. I say it’s okay, here’s the two functions. And you do your– You start the all the computations, step-by-step. Now remember you can’t do a derivative with the division side, you can’t do an integral with the division sign. You have to change it, there’s always rules in calculus and all the things they do change it to the basics of calculus, which is the derivative you know, multiplying that function times the exponent, subtracting one from the exponent. And then, in integration, adding one to the exponent, dividing by that answer. So know those in it because that’s what every calculation comes down to is to be able to do that, okay. And so we we keep going here, get to the answer here, very good, this is the answer. You write that on your paper, you just got an A on that problem without any effort. Right, if you want to compute that at a point I even have that in here for you. So we’re gonna compute it at– for instance, let’s go, alpha, and put in 3 for x. Again, I show you what you’ve entered in case you made a mistake. Let’s do that. We’re gonna go back and… alpha, let’s put another one in, let’s put in 4. You’re computing it at 4 of x, okay. I say it’s okay. And here’s the– you enter 4 for every x in that derivative. Here’s the prime of x which shows you the derivative, and then we’re entering 4, etc. And here’s the answer: -35 over 1296. Now this is the slope of a line, congratulations. 650 pages in a calculus book to come to this point. A slope of a line. So what do you have here? If you go -35 increments on the y-axis all the way down to -35, and then to the right because it’s positive on the x-axis, 1296.. this is slope. This is rise over run, okay, so you go over 1200 calculate increments all the way on the x-axis, draw a line from that point, through the origin of the graph, and that’s what you found as the slope of a line. That’s what you found the derivative… not tangent yet, because it goes through the origin of the graph. Pretty neat, huh? Everystepcalculus.com, go to my site, subscribe, and enjoy your calculus.

U Substitution Calculator

March 6, 2015 by Tommy Leave a Comment

Raw Transcript

Hello, everyone. Tomfrom everystepcalculus.com and everystepphysics.com. I’m already at U Substitution. You scroll with these cursors, here to get to whatever in my menu that you’re interested in. You have to press alpha before you enter anything into these entry lines, here. And the problem is Alpha x times the square root of x squared plus sixteen. close off the parentheses. X times Square root of x squared plus sixteen. That’s cool. I always show you what you’ve entered. Now, how are you going to go about solving this yourself? Okay, think about it. In U Substitution notice this is a exponent of two, this is an exponent of one. okay. If the x has one less exponent than the inside of the parentheses, this is a U substitution problem. For instance, you should always in your mind to do with the derivative of something in the parentheses in Calculus. That’s one of the big deals and big tricks. So this is 2 X then. And there’s of course no derivative 16 at zero. So it’s 2x

Well here’s an X on the outside. Well, we can do something with the 2 to make

that x dx. So generally what I do what and what you should do. I say it’s okay because we’ve entered it right. You should rewrite the problem okay. So you rewrite the problem.

Square root of x squared plus 16 and you put the x dx over here so you can kinda see that you’re trying to match that somehow, okay. So then U equals x squared plus 16. Well then du equals 2x dx, okay. We take that 2 and the du divided by 2 through Algebra. And we come up with x dx. Notice that this matches the previous match of the function. so that a course you is equal to this group experts 16 So we have the Integral of u and of course the square root, in calculus you always change it to 1/2. It was a cube, it could be 1/3. If it was the 15 root, you’d be 1/15, okay. That’s Algebra 2. I mean also. So and then you have the DU divided by two so that’s a constant, you have to bring outside the integral, here. I do that for you. Here’s the 1/2 outside the integral and then we do the U to the 1/2 inside and

then integrate that part, okay. And that turns out to be this this this and the answer is 1/3, etc. So, have a good one. everystepcalculus.com

Integral Calculator with Steps

March 4, 2015 by Tommy Leave a Comment

∫ 6x^4*(3x^5+2)^6 dx

Raw Transcript

Hello, everyone. This is Tom from everystepcalculus.com. There’s been many, there’s always requests for Integral Calculator with Steps and that’s exactly what my programs do. And Integration is one of the toughest things in Calculus. It was for me when I was in class. I hated

Calculus. You probably feel the same way and I’ve found nobody that likes Calculus. Except

maybe Professors. But anyways, I’m going to show you how my programs work on U Substitution. Index 8 to get to my menu. I’m already at U Substitution. I have scrolled there. We’re going to enter our function. You have to press Alpha before you enter anything into these entry lines, here. Alpha 6 times x to the fourth power times the quantity parentheses

3 times x to the fifth power plus 2, close off the parentheses to the sixth power. I always show you what you’ve entered. 6x 4 times 3 x quantive to the 5 plus 2 to 6. Looks good to me. I say it’s okay. And we’re going to work the problem. Busy means the program is loading. We’re going to evaluate this. First we rewrite it where all constants come out of the integral. And then we put the x to the 4. The way that you know that any problem is U Substitution is that you look immediately at what’s inside the parentheses. You take the derivative, right now you should be able to do, this is 15x to the 4. Right now in one second, you should be able to know the derivative of that. And you notice that x4 is on the outside, too. If it isn’t, it’s not a U Substitution problem. It has to be converted, okay. So I do all that for you, really. But that you have some understanding of how you do U Substitution. U is equal to this, du is equal to this and then we make this the other trick, this whole system here took me about a year to figure this out in a system that works, you know. And so, this always has to be x to the 4 dx over here so you have to take the 15 and divide the du by that on the other side using Algebra, of

course. And so it works the problem. 6, you take of course the du with the 6 here, you have a du with a 15 notice the 15 come out of the, here’s the constant again so that comes out of the integral and goes in front right here, see it right here. 6 times that, of course, with the 2 fifths. etc, etc. Here’s the answer to your problem right here. Have a good one. everystepcalculus.com

Integration by Parts

March 3, 2015 by Tommy Leave a Comment

Raw Transcript

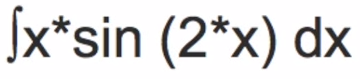
Hello, Tom from everystepcalculus.com and everystepphysics.com. This is a problem from a student regarding Transcendental Integrations. And it involves sin. So, I’m going to show you how my programs do that. Index eight to get to the menu, main menu. I’m already scrolled to integration by parts. Generally they give you that in the problem, in a test or. I’m gonna choose sin here because that’s what the problem is. You can see the problem on your screen. And we enter the problem, here. We have to press alpha before you enter anything in these entry lines in my programs Alpha X times second sin 2 times x. I always show you what you’ve entered, you can change it if you want. Just a little bit
of teaching which I don’t really do in my programs. I show rather than teach. Professors teach and then test on mechanics. I like to show the mechanics because that’s what I needed to pass my classes. So, why is this different? Why is this integration by parts and not U Substitution? Okay well get used to memorizing the derivative of anything inside of function Right away. For instance, like this sin of 2 X here is the derivative of that is 2 times the cosine of 2 x divided, oh no it’s not divided by it’s just a it’s just a 2 times the cosine of x. Well you notice there’s no X there, okay. There has to be an x because it has to match in U Substitution. This x and this DX here. Okay. So all we get here would be 2 DX
and so there’s no X involved in the derivative of this here. Therefore you can’t use U Substitution. So it’s integration by parts which is a different formula so I’m going to keep going and I’ll show. say it’s okay. Integration by parts, you come up DV which is the already the derivative of the sin of 2x and then you’re going to integrate that to get
minus cosine of 2x divided by 2, okay. And then U is equal to X and DU, the derivative of that is 1 DX. So now we do in the formula. vu minus the integral vdu dx, etc. Write all this entire paper exactly as you see it. And you’ll get a hundred percent here’s exactly this step by steps. And the answer is here. Careful now because like for instance minus x cosine of 2x divided by 2, a lot the calculator will come up with line here and do the denominator
by 2 you know and this will have the a line and the denominator is 4. So be hip to that when you’re looking at that because this is exactly the problem. Correct, right here. Alright, have a good one.