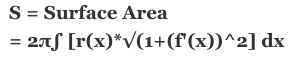Finding Derivative for Test Question-Video
Derivative of ln[x^(2/3)]
Raw Transcripts
Hello, everyone. This is Tom from everystepcalculus.com and everystepphysics.com. In this video,how to do the derivative of the log, natural log of some function. And you can see function on your screen. Let’s do it. Index 8 to get to my menu. And we’re already at log of x derivative. Scroll down to that. Press enter. And we’re going to differentiate it. Because that’s what we’re doing. We’re finding the derivative. And we enter our function. In this case, you have to press Alpha before you enter anything into these entry lines on my programs. I’m going to press alpha and then it’s second to get to the log function. Here’s log of our problem. And it’s X to the two-thirds. Close off the parentheses. I always show you what you’ve entered, you can change it if you want. I say it’s okay. You press number one. Here’s the formula. Here’s over after the derivative of this. U prime over U is the formula, etc. Pretty simple but to remember all these different formulas and rules in Calculus is very difficult. That’s the reason I needed to program this stuff. The answer is 2 over 3x. Pretty neat, huh? everystepcalculus.com. Go to my site and subscribe so you can see more videos that I made you. Have a good one.
Natural Log ln(x) Solved for Test-Video
Solve the Equation: ln(x+2)=3
Raw Transcripts
Hello, again. Tom from everystepcalculus.com and everystepphysics.com. I’m going to do a, solve a natural log equation right no, on the Titanium. I’ll show you my program work on that. Index 8 to get to my menu. I’m already at the scroll down to log of x solved. Press enter and number three. Choose number three solving. You have to go through the menus. We’re going to enter the function. You have press Alpha before you enter anything into these entry lines, here. Alpha second log of X plus 2 equals 3. I always show you what you’ve entered, in programs, you can change in case you made a mistake. I say it’s okay. You’re going to multiply both sides by E. And when you multiply a log times E, you get X plus 2 simply. These are all simple but try to remember that during a test with the other any number of equations and rules you have to memorize to place into a calculus test. Pretty neat, huh? everystepcalculus.com. Go to my site, buy my programs if you want to pass calculus and subscribe so you can see more videos.Have a good one.
Evaluate Log Problem on TI-89-Video
![]()
Raw Transcript
Hello, everyone. Tom from everystepcalculus.com and everystepphysics.com. I’m going to integrate a log to a base problem, in this video.Let’s do it. Index 8 to get to my menu. We’re going to use second and the cursor here to go to screen by screen to get down to the L section where there’s log problems. We’re going to choose that one. And here’s log problems. And we’re gonna, we want to integrate. So we’re going to choose integrate, number 9 there. You could press a number or scroll to it, either one. And we’re going to enter our functions, here. Now this is a little tricky because we have to add l o g in here. So we’re going to have to press second, Alpha twice so it this becomes black. You see this black here? Then we can go, 4 minus 7 is l o g. (Excuse me). And then we press Alpha to go back to the number register. And we’re going to put three and then they close parentheses or left parentheses, three times X and then the right parentheses. And I always show you what you’ve entered, you can change it if you want. I say it’s okay. Now in a log problem, you have to change it and ln(x) before you can integrate it so that’s this system here. In other words this goes in the log and you divide it by the log of the base, three. So then we’re into integration by parts and you mark all this stuff exactly as you see in your paper. Here’s the formula. VU minus the integral of VDU. And we keep working a problem multiplying things and whatever we have to do. And here’s the answer. Pretty neat, huh? everystepcalculus.com. Go to my site. You can see, I’m going to go back for just for a second. You can see all the things you can do solve for x or exponential form, logarithmic form, etc.
Calculus Derivative Difference Quotient-Video
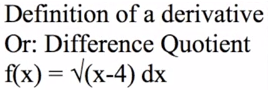
Raw Transcript
Hello, everyone. Tom from everystepcalculus.com and everystepphysics.com. I’m gonna do a a definition of the derivative or difference quotient problem right now. et’s do it. Index 8 to get to my menu. Scroll down to definition of a derivative. There it is there. I gave you a little bit of help in case your professor does some tricks change of X instead H. There’s all kind of tricks and this is one of the most nonsensical things I’ve ever seen in calculus. It’s all nonsense but.. I’m going to choose number two, here. For a square root function. I’m going to enter the function. You have to press Alpha before you enter anything into these entry lines. Alpha, going to use the square root second square root of X minus 4, close off the parentheses. And I say it’s okay I give you a chance to change it in case you make a mistake. Here’s the formula. And remember, you’re replacing X plus H for every X in the function. And then in the case of square roots, you’re using the difference squares to get rid of the radical signs. So we’re multiplying it times the plus of the same thing which makes those squares. I’ll show you that in the next one, here. So they become squares and when you square a square root, you get what’s inside the square root. Here it is. And in the bottom, of course H, you do the same thing because they’re really taking the numerator and denominator exactly the same thing which you have to do So you don’t change the function. And then on the top, we multiply it all together. And you come up with H on the top, these H’s cancel. Becomes one and now we’re gonna when H equals 0, then we apply that to this down here which cleans that up and makes it the same thing. Two of each right here. So that’s where the two comes into it. Here’s the answer one over two times square root of x minus 4. As usual, calculus makes a big big deal about this when
Line Integral r(t) Points Showing Work on TI-89-Video

Raw Transcript
Hello, everyone. Tom from everystepcalculus.com and everystepphysics.com. A problem on line integral, today from my menu. And this is off the internet from Patrick JMT. So, he’s my favorite. Um, let’s do it. Index 8 to get to my menu. And we gotta press second and the cursor down so you can go screen by screen to get to the L section. Which is Line Integral, here. And since they give us rt in the problem, you can see the problem on your screen. We choose RT from the menu. And that was the, um. Let’s go back and look at that menu, quick. Notice we have RT which is the original function XT plus YT plus ZT and then we have the magnitude of this of the derivative of that. But in other words, here’s exactly what it is. XT, YT, ZT which is the function there times the magnitude which is x prime of t squared, y prime of t squared, z prime of t squared. Write this all on your paper, of course. We’re going to enter our function. You have to press Alpha before you enter anything into these entry lines. You’re going to press Alpha 2 times x times y plus 3 times z. Again, I show you what you’ve entered. You can change it if you’ve made a mistake. Looks pretty good. Now we’re going to enter our lower point from the problem. So you’re going to press Alpha 0, 0, 0. I say it’s okay. Upper limit or point. Alpha 2, 5, 4. Now notice that the farthest point, really really we’re taking so it’s different from 0 0 0 in the beginning point, we would subtract the beginning from the end point here. And then when you integrate this with respect to T, that’s where the whole system starts. Then we get XT which is 2t, 5t, and 4t. Then we start putting it together here. Here’s the original function XT, YT, ZT and the magnitude square root of 45. And then we, in integration, we always take the constants out of the integral before you work the integral. So, we factored the inside, took the 4 out and the square root of 45 out and this is what is left here for integration. So we’re going to integrate that, you know add 1 to the 2 here to get 3 and divide by 3. And so then we have this here which we’re going to do over the limit of 1 to 0. Write all this down, this is exactly the way it’s done. T equals 1 then. Substitute 1 for all the t’s in the integral. And so here, I use quotation marks here because of the calculator but you’re going to use parentheses when you put this on your paper. So you look like you know what you’re doing. These calculations are exactly right. We come up with 38 times the square root of 5. And then at t = 0 and here’s the replacements of t with all the zeroes in it and that of course equals zero. We’re going to take the upper minus the lower which is 38 square root of 5 minus 0. So the answer is 38 square root of 5.
Finding Natural Log Showing Work on TI89-Video
What is the integral of ln(x^2+2*x) dx?
Raw Transcript
Critical Points-Work Shown on TI-89-Video
Transcripts
Hello, Tom from everystepcalculus.com,and everystepphysics.com. A problem in calculus dealing with critical numbers in critical points of a function. Let’s do it. Index 8 to get to my menu. Then your going to scroll down to critical point or numbers.I always have you start a graph on your paper. When you enter the function you have to press Alpha before you enter anything into these entry lines. Your going to press Alpha X cubed minus 3 times X. I always show you what you’ve entered. You can change it if you want. I say it’s okay. And we’re gonna choose number five, critical points.
What is Parametric Equation?-Video
Transcript
This video is on parametric equations. A parametric equation is, you’re adding a parameter of t time to every x y and z function, and that’s where we add the parameter and that’s the reason we call them parametric equations. And let’s do it. Turn the calculator on here. We’re going to get back to the home screen here. Clear the calculator we can go F1 eight and it clears that screen here. You press second alpha and put in the letters i n d e x, and then you push alpha and get into the number 8 and closed parenthesis to add this and get my formula for my menu. Press enter and we’re into my menu. And you can see all the things available in my menu for you to pass calculus and do your homework. Position vectors, product rule, projection of a and b, all those kinds of things you will be involved with in calculus one two or three. We’re going to do parametric equations now. That’s concerned with position vectors. If z is not given you enter zero in for z, then you can do the other two, x and y. So there’s the vector r t is generally an r t, is equal to this vector here, x t, y t and z t. So you have to press alpha to enter the functions in the entry lines here, so let’s do it, three times t let’s say plus four for x t, here’s y t, let’s enter have to push alpha, five times t and let’s do the z one, or let’s put alpha just for to make it simple and put z you can see that the z one is zero. Gives you a chance to change it if you’ve made a mistake, and we have all these things that we can do with this formula now with these functions in there. We can eliminate the parameter. Which eliminates the t and changes it back to an x function. Let’s do that quick, I’ll go through these quick so you can see. You solve for t, here’s the solution for t, and then you substitute t into every other x y and z, but ah here’s one point six seven times x minus three point nine and that eliminated the t parameter. Let’s go length of arc, you want to do that, fine, let’s go press four, notice it’s an integral over a and b, with the derivative of the r t formula. And rt we’re going to put in what we entered, I’ll go through it quick, put this all on your paper, write it down exactly as you see it, and we’re doing the square of each one, over the time of let’s say, you have to push alpha, let’s say from two to alpha six, shows you from two to six, here we’re doing this, write this on your paper and each individual one is gone, there it is, and here we substitute etcetera in there, and here we have approximately twenty three point four units. We can do speed, do you wanna do speed, let’s push number seven here and do speed, unit vectors or speed is the square root of these squared. Square root of nine, twenty five zero. 5.8 meters per second. Ah pretty neat huh? everystepcalculus.com, check it out. Go to my site and you’ll love these programs.
Triple Integral: Work Shown on TI89-Video
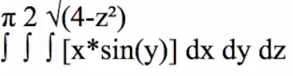
Transcripts
Hello again, everyone. This is Tom from everystepcalculus.com and everystepphysics.com. I’m going to do a Triple Integral for Calculus 3 right now. This is an example of a Patrick JMT, my favorite instructor on the internet, on YouTube. So I’m going to show you how it works on my program. I don’t know anybody can do that problem. He can do it because he’s a genius. But for us students,etc. How do we do it? Let’s get started. Index 8 to get to my menu. I’m going to scroll up because I can go to the bottom of the menu then instead of going down quicker to go to the T’s section. And we’re going to choose Triple Integral. And we’re going to enter our function. You have to press Alpha before you enter anything into these entry lines here in programs, okay. Alpha x times sin of Y. I always show you what you’ve entered. You can change it if you want. And we’re going to use the order of integration which is dx, dz, dy which is in the example. You have the other choices in case that’s given on test also. And we’re going to enter region q. Enter these limits. This is Alpha 0 for the x one Alpha square root of 4 minus z squared I made a mistake so I gotta go back. Choose number 2. Alpha 0, Alpha square root of 4 minus z squared. Close up the parentheses. That’s better. I say it’s okay. Next one for the y is Alpha 0. Alpha pi. That looks okay. and Alpha 0 for z. Alpha 2. That’s okay. So here’s what you write on your paper. The way you write it with triple integral with dx dz dy order of integration. Here’s the function in here. So you’re going to do the dx first and you put this over here with these lines. Showing you’r doing a range over this integration here. And here’s the integral of the first function okay. And if x equals the upper range. I show quotation marks here but you put you put parentheses in there. Because you’re substituting this amount for an X in the integral. And it equals this, minus sin, etc. And then we do the lower integral. X equals 0 and there’s 0 and you put parentheses around this instead of quotation marks, okay? And here’s the answer, you have the upper range minus the lower range equals this right here. So that becomes the new integration function. And I show you that here. dz dy is left, okay. So now we integrate that. Come up with this. Minus sin, etc. over this range here 0 2. Add z equals 2 Here’s the answer here. And z equals 0. Plug these in for all the Z’s in the problem. And the answer is this. 8, the upper range minus the lower range is 8 sin y divided by 3. Now we’re going to use that for the integration function. With the range of 0 and pi. At y equals pi minus 8 cosine is 8 thirds.
Surface of Area of Revolution-Video
Transcript
A problem in calculus called Surface Area of a Revolution. So let’s do it. Index 8 to get to my menu. We’re going to go up to get to the bottom of the alphabet. And scroll up to Surface Area of Revolution.
We’re going to enter our, I’ll show you the actual formula here. Let’s write down your paper first. Press Alpha to enter anything into these entry lines here. Alpha x cubed over the range of alpa zero for a for b, Alpha 2. I show you what you’ve entered so you can change it if you want. I say it’s okay. The first derivative is 3x squared. That goes into the formula here. That’s part of the formula. Over 0 and 2 for the range. And we start doing the computations. Squaring things. This is U Substitution. U equals this. DU equals 36. You always take 36 and put it on the other side as a denominator. DU/36 equals that. And this x cubed equals the problem. X cubed dx. And then we substitute for U. In the problem here, DU 36 has to come out of the integral. So that 2 pi, there’s the 1 over 36 here and that computes to pi over 18, etc. We’re doing the integral of one half, of course you add two halves to that and Upper Range less than the Lower Range. And you get 203 squared units. Pretty neat, huh? everystepcalculus.com. Go to my site, subscribe to see more videos or go to the menu and look up what you need to learn about and pass your calculus. Have a good one.
Find the Gradient of Point-Video
Given Vectors A&B find Projection A on B-Video
Find the gradient of
f(x,y,z)=x^2+y^2-4z, at the point (2,-1,1)
Unit Vector with P & Q Points Q to P
L’hospitals Rule Using Limits to Infinity
Gradient Solver at Point (1,2) Video
L’hospitals Rule & Indeterminate Quotients-Video
Unit Vector With P&Q Points-Video
Length of a Vector Using P&Q Points-Video
Triple Integral dz, dy, dx Solver-Video
- « Previous Page
- 1
- …
- 3
- 4
- 5
- 6
- 7
- …
- 16
- Next Page »